BDS Independence Test
This series view carries out the BDS test for independence as described in Brock, Dechert, Scheinkman and LeBaron (1996).
The BDS test is a portmanteau test for time based dependence in a series. It can be used for testing against a variety of possible deviations from independence including linear dependence, non-linear dependence, or chaos.
The test can be applied to a series of estimated residuals to check whether the residuals are independent and identically distributed (iid). For example, the residuals from an ARMA model can be tested to see if there is any non-linear dependence in the series after the linear ARMA model has been fitted.
The idea behind the test is fairly simple. To perform the test, we first choose a distance,
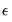
. We then consider a pair of points. If the observations of the series truly are
iid, then for any pair of points, the probability of the distance between these points being less than or equal to epsilon will be constant. We denote this probability by
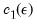
.
We can also consider sets consisting of multiple pairs of points. One way we can choose sets of pairs is to move through the consecutive observations of the sample in order. That is, given an observation
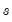
, and an observation
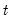
of a series
X, we can construct a set of pairs of the form:
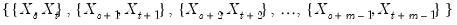 | (42.98) |
where
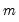
is the number of consecutive points used in the set, or
embedding dimension. We denote the joint probability of every pair of points in the set satisfying the epsilon condition by the probability
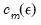
.
The BDS test proceeds by noting that under the assumption of independence, this probability will simply be the product of the individual probabilities for each pair. That is, if the observations are independent,
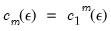 | (42.99) |
When working with sample data, we do not directly observe
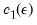
or
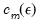
. We can only estimate them from the sample. As a result, we do not expect this relationship to hold exactly, but only with some error. The larger the error, the less likely it is that the error is caused by random sample variation. The BDS test provides a formal basis for judging the size of this error.
To estimate the probability for a particular dimension, we simply go through all the possible sets of that length that can be drawn from the sample and count the number of sets which satisfy the
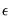
condition. The ratio of the number of sets satisfying the condition divided by the total number of sets provides the estimate of the probability. Given a sample of
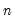
observations of a series X, we can state this condition in mathematical notation,
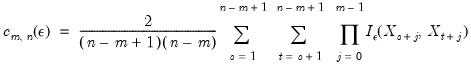 | (42.100) |
where
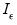
is the indicator function:
 | (42.101) |
Note that the statistics
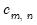
are often referred to as
correlation integrals.
We can then use these sample estimates of the probabilities to construct a test statistic for independence:
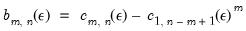 | (42.102) |
where the second term discards the last
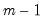
observations from the sample so that it is based on the same number of terms as the first statistic.
Under the assumption of independence, we would expect this statistic to be close to zero. In fact, it is shown in Brock et al. (1996) that
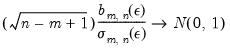 | (42.103) |
where
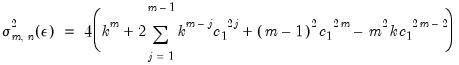 | (42.104) |
and where
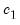
can be estimated using
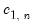
.
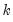
is the probability of any triplet of points lying within
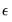
of each other, and is estimated by counting the number of sets satisfying the sample condition:
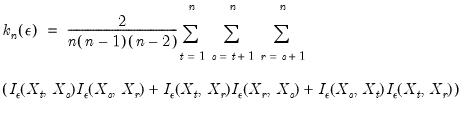 | (42.105) |
To calculate the BDS test statistic in EViews, simply open the series you would like to test in a window, and choose . A dialog will appear prompting you to input options.
To carry out the test, we must choose
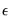
, the distance used for testing proximity of the data points, and the dimension
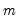
, the number of consecutive data points to include in the set.
The dialog provides several choices for how to specify
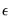
:
• Fraction of pairs:
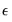
is calculated so as to ensure a certain fraction of the total number of pairs of points in the sample lie within
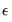
of each other.
• Fixed value:
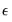
is fixed at a raw value specified in the units as the data series.
• Standard deviations:
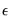
is calculated as a multiple of the standard deviation of the series.
• Fraction of range:
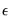
is calculated as a fraction of the range (the difference between the maximum and minimum value) of the series.
The default is to specify
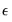
as a fraction of pairs, since this method is most invariant to different distributions of the underlying series.
You must also specify the value used in calculating
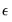
. The meaning of this value varies based on the choice of method. The default value of 0.7 provides a good starting point for the default method when testing shorter dimensions. For testing longer dimensions, you should generally increase the value of
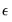
to improve the power of the test.
EViews also allows you to specify the maximum correlation dimension for which to calculate the test statistic. EViews will calculate the BDS test statistic for all dimensions from 2 to the specified value, using the same value of
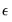
or each dimension. Note the same
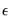
is used only because of calculational efficiency. It may be better to vary
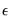
with the correlation dimension to maximize the power of the test.
In small samples or in series that have unusual distributions, the distribution of the BDS test statistic can be quite different from the asymptotic normal distribution. To compensate for this, EViews offers you the option of calculating bootstrapped p-values for the test statistic. To request bootstrapped p-values, simply check the Use bootstrap box, then specify the number of repetitions in the field below. A greater number of repetitions will provide a more accurate estimate of the p-values, but the procedure will take longer to perform.
When bootstrapped p-values are requested, EViews first calculates the test statistic for the data in the order in which it appears in the sample. EViews then carries out a set of repetitions where for each repetition a set of observations is randomly drawn with replacement from the original data. Also note that the set of observations will be of the same size as the original data. For each repetition, EViews recalculates the BDS test statistic for the randomly drawn data, then compares the statistic to that obtained from the original data. When all the repetitions are complete, EViews forms the final estimate of the bootstrapped p-value by dividing the lesser of the number of repetitions above or below the original statistic by the total number of repetitions, then multiplying by two (to account for the two tails).
As an example of a series where the BDS statistic will reject independence, consider a series generated by the non-linear moving average model:
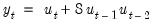 | (42.106) |
where
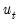
is a normal random variable. On simulated data, the correlogram of this series shows no statistically significant correlations, yet the BDS test strongly rejects the hypothesis that the observations of the series are independent (note that the
Q-statistics on the squared levels of the series also reject independence).
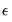 . We then consider a pair of points. If the observations of the series truly are iid, then for any pair of points, the probability of the distance between these points being less than or equal to epsilon will be constant. We denote this probability by
. We then consider a pair of points. If the observations of the series truly are iid, then for any pair of points, the probability of the distance between these points being less than or equal to epsilon will be constant. We denote this probability by 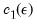 .
.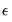 . We then consider a pair of points. If the observations of the series truly are iid, then for any pair of points, the probability of the distance between these points being less than or equal to epsilon will be constant. We denote this probability by
. We then consider a pair of points. If the observations of the series truly are iid, then for any pair of points, the probability of the distance between these points being less than or equal to epsilon will be constant. We denote this probability by 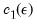 .
.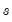 , and an observation
, and an observation 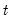 of a series
of a series 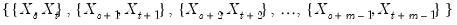
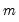 is the number of consecutive points used in the set, or
is the number of consecutive points used in the set, or 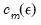 .
.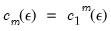
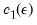 or
or 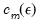 . We can only estimate them from the sample. As a result, we do not expect this relationship to hold exactly, but only with some error. The larger the error, the less likely it is that the error is caused by random sample variation. The BDS test provides a formal basis for judging the size of this error.
. We can only estimate them from the sample. As a result, we do not expect this relationship to hold exactly, but only with some error. The larger the error, the less likely it is that the error is caused by random sample variation. The BDS test provides a formal basis for judging the size of this error.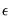 condition. The ratio of the number of sets satisfying the condition divided by the total number of sets provides the estimate of the probability. Given a sample of
condition. The ratio of the number of sets satisfying the condition divided by the total number of sets provides the estimate of the probability. Given a sample of 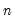 observations of a series X, we can state this condition in mathematical notation,
observations of a series X, we can state this condition in mathematical notation,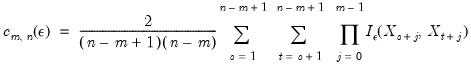
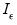 is the indicator function:
is the indicator function:
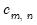 are often referred to as
are often referred to as 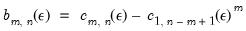
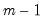 observations from the sample so that it is based on the same number of terms as the first statistic.
observations from the sample so that it is based on the same number of terms as the first statistic. 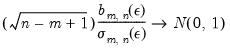
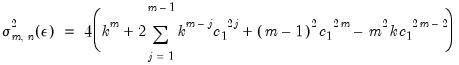
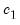 can be estimated using
can be estimated using 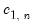 .
. 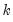 is the probability of any triplet of points lying within
is the probability of any triplet of points lying within 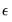 of each other, and is estimated by counting the number of sets satisfying the sample condition:
of each other, and is estimated by counting the number of sets satisfying the sample condition: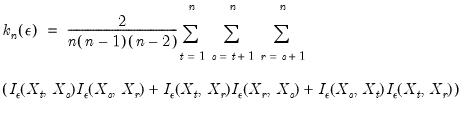
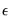 , the distance used for testing proximity of the data points, and the dimension
, the distance used for testing proximity of the data points, and the dimension 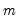 , the number of consecutive data points to include in the set.
, the number of consecutive data points to include in the set.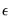 :
: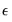 is calculated so as to ensure a certain fraction of the total number of pairs of points in the sample lie within
is calculated so as to ensure a certain fraction of the total number of pairs of points in the sample lie within 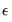 of each other.
of each other.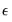 is fixed at a raw value specified in the units as the data series.
is fixed at a raw value specified in the units as the data series.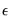 is calculated as a multiple of the standard deviation of the series.
is calculated as a multiple of the standard deviation of the series.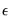 is calculated as a fraction of the range (the difference between the maximum and minimum value) of the series.
is calculated as a fraction of the range (the difference between the maximum and minimum value) of the series.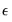 as a fraction of pairs, since this method is most invariant to different distributions of the underlying series.
as a fraction of pairs, since this method is most invariant to different distributions of the underlying series.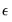 . The meaning of this value varies based on the choice of method. The default value of 0.7 provides a good starting point for the default method when testing shorter dimensions. For testing longer dimensions, you should generally increase the value of
. The meaning of this value varies based on the choice of method. The default value of 0.7 provides a good starting point for the default method when testing shorter dimensions. For testing longer dimensions, you should generally increase the value of 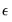 to improve the power of the test.
to improve the power of the test.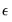 or each dimension. Note the same
or each dimension. Note the same 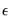 is used only because of calculational efficiency. It may be better to vary
is used only because of calculational efficiency. It may be better to vary 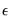 with the correlation dimension to maximize the power of the test.
with the correlation dimension to maximize the power of the test.
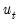 is a normal random variable. On simulated data, the correlogram of this series shows no statistically significant correlations, yet the BDS test strongly rejects the hypothesis that the observations of the series are independent (note that the
is a normal random variable. On simulated data, the correlogram of this series shows no statistically significant correlations, yet the BDS test strongly rejects the hypothesis that the observations of the series are independent (note that the