Seed the random number generator.
Use rndseed when you wish to generate a repeatable sequence of random numbers, or to select the generator to be used.
Note that EViews 5 has updated the seeding routines of two of our pseudo-random number generators (backward compatible options are provided). It is strongly recommended that you use new generators.
Syntax
rndseed(options) integer
Follow the rndseed keyword with the optional generator type and an integer for the seed.
Options
type=arg (default=“kn”) | Type of random number generator: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4)”, L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
When EViews starts up, the default generator type is set to the improved Knuth lagged Fibonacci generator. Unless changed using rndseed, Knuth’s generator will be used for subsequent pseudo-random number generation.
| Knuth (“kn4”) | L’Ecuyer (“le”) | Mersenne Twister (“mt4”) |
Period | | | |
Time (for 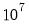 draws) | 27.3 secs | 15.7 secs | 1.76 secs |
Cases failed Diehard test | 0 | 0 | 0 |
Examples
rndseed 123456
genr t3=@qtdist(rnd,3)
rndseed 123456
genr t30=@qtdist(rnd,30)
generates random draws from a t-distribution with 3 and 30 degrees of freedom using the same seed.
Cross-references
See the list of available random number generators in
“Statistical Distribution Functions”.
At press time, further information on the improved seeds may be found on the web at the following addresses:
See also
nrnd,
rnd and
rndint.
References
Knuth, D. E. (1997). The Art of Computer Programming, Volume 2, Semi-numerical Algorithms, 3rd edition, Reading, MA: Addison-Wesley Publishing Company. Note: the C implementation of the lagged Fibonacci generator is described in the errata to the 2nd edition, downloadable from Knuth's web site.
L’Ecuyer, P. (1999). “Good Parameters and Implementations for Combined Multiple Recursive Random Number Generators,” Operations Research, 47(1), 159-164
Matsumoto, M. and T. Nishimura (1998). “Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator,” ACM Transactions on Modeling and Computer Simulation, 8(1), 3-30.
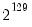


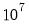 draws)
draws)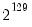


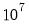 draws)
draws)