We can use the estimated equation to perform hypothesis tests on the coefficients of the model. For example, to test the hypothesis that the coefficient on the price term is equal to 2, we will perform a Wald test. First, determine the coefficient of interest by selecting View/Representations from the equation toolbar:

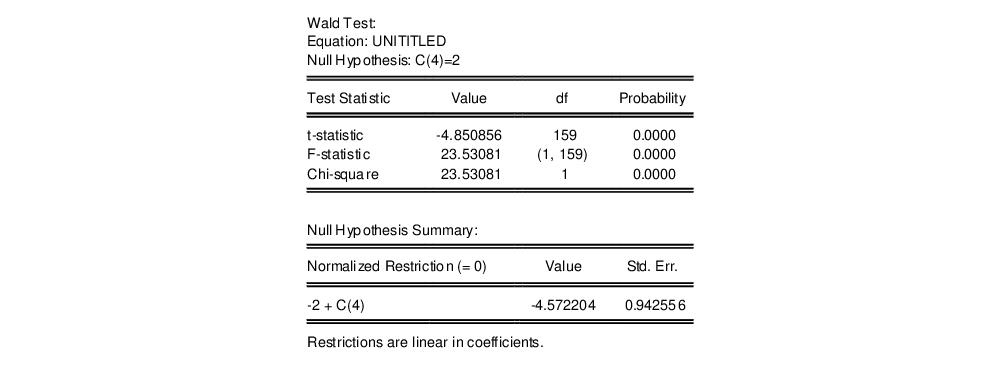
Note that the coefficients are assigned in the order that the variables appear in the specification so that the coefficient for the PR term is labeled C(4). To test the restriction on C(4) you should select View/Coefficient Diagnostics/Wald Test–Coefficient Restrictions…, and enter the restriction “c(4)=2”. EViews will report the results of the Wald test:

The low probability values indicate that the null hypothesis that C(4)=2 is strongly rejected.

We should, however, be somewhat cautious of accepting this result without additional analysis. The low value of the Durbin-Watson statistic reported above is indicative of the presence of serial correlation in the residuals of the estimated equation. If uncorrected, serial correlation in the residuals will lead to incorrect estimates of the standard errors, and invalid statistical inference for the coefficients of the equation.

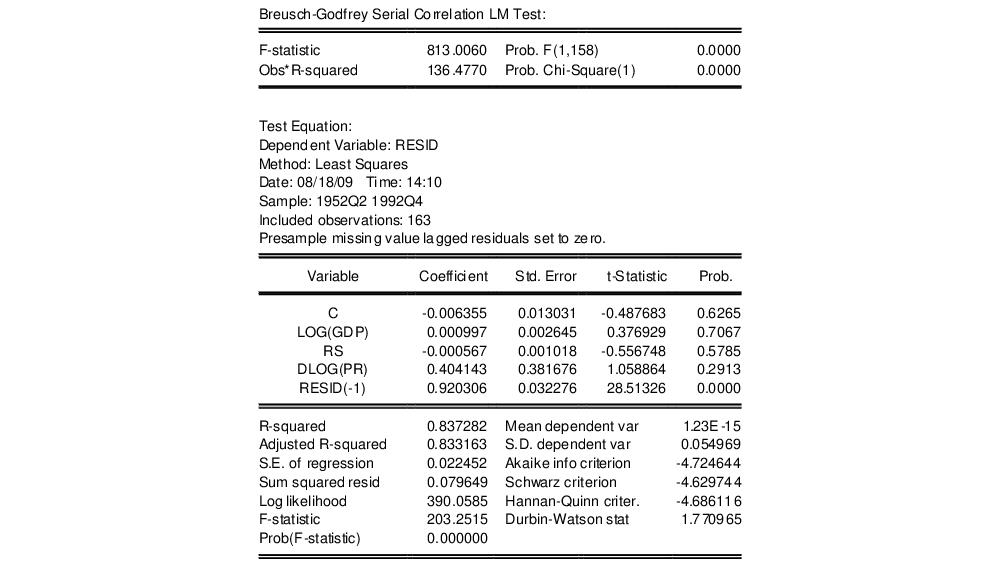
The Durbin-Watson statistic can be difficult to interpret. To perform a more general Breusch-Godfrey test for serial correlation in the residuals, select View/Residual Diagnostics/Serial Correlation LM Test… from the equation toolbar, and specify an order of serial correlation to test against. Entering “1” yields a test against first-order serial correlation:

The top part of the output presents the test statistics and associated probability values. The test regression used to carry out the test is reported below the statistics.

The statistic labeled “Obs*R-squared” is the LM test statistic for the null hypothesis of no serial correlation. The (effectively) zero probability value strongly indicates the presence of serial correlation in the residuals.