Estimation by discrete or smooth threshold least squares, including threshold autoregression.
Syntax
eq_name.threshold(options) y z1 [z2 z3 ...] [@nv x1 x2 x3 ...] @thresh t1 [t2 t3 ...]
List the dependent variable first, followed by a list of the independent variables that have coefficients that are allowed to vary across threshold, followed optionally by the keyword @nv and a list of non-varying coefficient variables.
List a threshold variable or variables (for model selection) or a single integer or range pairs after the keyword @thresh. The integer or range pairs indicate a self-exciting model with the lagged dependent variable as the threshold variable.
For smooth threshold equations you may specify variables that are to be included only in the base specification or only in the alternative specification. Base-only variables should be specified in parentheses using the @base key, as in “@base(x1) @base(x2) @base(x3 x4)”. Alternative-only variables may be specified analogously using the @alt key.
Options
Specification Options
type=arg (default=“discrete”) | Type of threshold estimation: “discrete” (discrete), “smooth” (smooth). |
Discrete Threshold Options
method=arg (default=“seqplus1”) | Threshold selection method: “seqplus1” (sequential tests of single 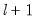 versus 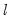 thresholds), “seqall” (sequential test of all possible 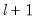 versus 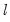 thresholds), “glob” (tests of global 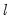 vs. no thresholds), “globplus1” (tests of 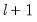 versus 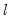 globally determined thresholds), “globinfo” (information criteria evaluation)., “fixedseq” (fixed number of sequentially determined thresholds), “fixedglob” (fixed number of globally determined thresholds), “user” (user-specified thresholds) |
nthresh=arg (default=1) | Number of thresholds for fixed number threshold selection methods. |
select=arg | Sub-method setting (options depend on “method=”). (1) if “method=glob”: Sequential ("seq") (default), Highest significant ("high"), 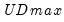 ("udmax"), 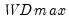 ("wdmax"). (2) if “method=globinfo”: Schwarz criterion (“bic” or “sic”) (default), Liu-Wu-Zidek criterion (“lwz”). |
trim=arg (default=5) | Trimming percentage for determining minimum segment size (5, 10, 15, 20, 25). |
maxthresh=integer (default=5) | Maximum number of thresholds to allow (not applicable if “method=seqall”). |
maxlevels=integer (default=5) | Maximum number of threshold levels to consider in sequential testing (applicable when “method=sequall”). |
size=arg (default=5) | Test sizes for use in sequential determination and final test evaluation (10, 5, 2.5, 1) corresponding to 0.10, 0.05, 0.025, 0.01, respectively |
heterr | Assume regimes specific error distributions in variance computation. |
commondata | Assume a common distribution for the data across segments (only applicable if original equation is estimated with a robust covariance method, “heterr” is not specified). |
Smooth Threshold Options
smoothtrans=arg (default=“logistic”) | Smooth threshold transition function: “logistic” (logistic), “logistic2” (second-order logistic), “exponential” (exponential), “normal” (normal). |
smoothstart=arg (default=“grid_conc”) | Smoth threshold starting value method: or fixed number threshold selection methods: “grid_conc” (grid search with concentrated regression coefficients”, “grid_zeros” (grid search with zero regression coefficients), “data” (data-based), “user” (user-specified using the contents of the coefficient vector in the workfile). |
smoothst=arg | Sub-method setting (options depend on “method=”). (1) if “method=glob”: Sequential ("seq") (default), Highest significant ("high"), 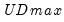 ("udmax"), 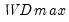 ("wdmax"). (2) if “method=globinfo”: Schwarz criterion (“bic” or “sic”) (default), Liu-Wu-Zidek criterion (“lwz”). |
General Options
w=arg | Weight series or expression. |
wtype=arg (default=“istdev”) | Weight specification type: inverse standard deviation (“istdev”), inverse variance (“ivar”), standard deviation (“stdev”), variance (“var”). |
wscale=arg | Weight scaling: EViews default (“eviews”), average (“avg”), none (“none”). The default setting depends upon the weight type: “eviews” if “wtype=istdev”, “avg” for all others. |
cov=keyword | Covariance type (optional): “white” (White diagonal matrix), “hac” (Newey-West HAC). |
nodf | Do not perform degree of freedom corrections in computing coefficient covariance matrix. The default is to use degree of freedom corrections. |
covlag=arg (default=1) | Whitening lag specification: integer (user-specified lag value), “a” (automatic selection). |
covinfosel=arg (default=“aic”) | Information criterion for automatic selection: “aic” (Akaike), “sic” (Schwarz), “hqc” (Hannan-Quinn) (if “lag=a”). |
covmaxlag=integer | Maximum lag-length for automatic selection (optional) (if “lag=a”). The default is an observation-based maximum of  . |
covkern=arg (default=“bart”) | Kernel shape: “none” (no kernel), “bart” (Bartlett, default), “bohman” (Bohman), “daniell” (Daniel), “parzen” (Parzen), “parzriesz” (Parzen-Riesz), “parzgeo” (Parzen-Geometric), “parzcauchy” (Parzen-Cauchy), “quadspec” (Quadratic Spectral), “trunc” (Truncated), “thamm” (Tukey-Hamming), “thann” (Tukey-Hanning), “tparz” (Tukey-Parzen). |
covbw=arg (default=“fixednw”) | Kernel Bandwidth: “fixednw” (Newey-West fixed), “andrews” (Andrews automatic), “neweywest” (Newey-West automatic), number (User-specified bandwidth). |
covnwlag=integer | Newey-West lag-selection parameter for use in nonparametric kernel bandwidth selection (if “covbw=neweywest”). |
covbwint | Use integer portion of bandwidth. |
prompt | Force the dialog to appear from within a program. |
p | Print basic estimation results. |
Examples
equation eq1.threshold(method=fixedseq, type=discrete) ss_transf c ss_transf(-1 to -11) @thresh 2
uses the fixed number of thresholds test to determine the optimal threshold in a model regressing SS_TRANSF on the threshold variables C and SS_TRANSF(-1 to -11).
equation eq2.threshold(method=fixedseq, type=discrete) ss_transf c ss_transf(-1 to -11) @thresh 1 5
uses the fixed number of thresholds test to determine the optimal threshold and does model selection over lags of SS_TRANSF from SS_TRANSF(-1) to SS_TRANSF(-5).
equation eq3.threshold(method=user, threshold=7.44) ss_transf c @nv ss_transf(-1 to -11) @thresh 2
estimates the model with one user-specified threshold value. In addition, the variables SS_TRANSF(-1 to -11) are restricted to have common coefficients across the regimes.
Cross-references
See
“Discrete Threshold Regression” and
“Smooth Transition Regression” for a discussion of the various forms of threshold models.
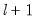 versus
versus 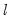 thresholds), “seqall” (sequential test of all possible
thresholds), “seqall” (sequential test of all possible 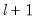 versus
versus 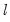 thresholds), “glob” (tests of global
thresholds), “glob” (tests of global 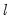 vs. no thresholds), “globplus1” (tests of
vs. no thresholds), “globplus1” (tests of 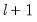 versus
versus 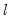 globally determined thresholds), “globinfo” (information criteria evaluation)., “fixedseq” (fixed number of sequentially determined thresholds), “fixedglob” (fixed number of globally determined thresholds), “user” (user-specified thresholds)
globally determined thresholds), “globinfo” (information criteria evaluation)., “fixedseq” (fixed number of sequentially determined thresholds), “fixedglob” (fixed number of globally determined thresholds), “user” (user-specified thresholds)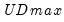 ("udmax"),
("udmax"), 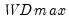 ("wdmax").
("wdmax").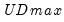 ("udmax"),
("udmax"), 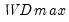 ("wdmax").
("wdmax"). .
.