Name | Function | Description |
@cumdn(x, d[, y, s]) | cumulative negative (below threshold) changes | cumulative process of changes in X from date D, for observations with negative (or below Y threshold) changes. |
@cumdp(x, d[, y, s]) | cumulative positive (above threshold) changes | cumulative process of changes in X from date D, for observations with positive (or below Y threshold) changes. |
@cumdz(x, d[, y, s]) | cumulative zero (at threshold) changes | cumulative process of changes in X from date D, for observations with positive (or at Y threshold) changes. |
@cumsum(x[,s]) | cumulative sum | cumulative sum of the values in X from the start of the workfile/sample. |
@cumprod(x[,s]) | cumulative product | cumulative product of the values in X from the start of the workfile/sample (note this function could be subject to numerical overflows). |
@cummean(x[,s]) | cumulative mean | mean of the values in X from the start of the workfile/sample to the current observation. |
@cumstdev(x[,s]) | cumulative standard deviation | sample standard deviation of the values in X from the start of the workfile/sample to the current observation. Note this calculation involves division by 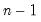 . . |
@cumstdevp(x[,s]) | cumulative population standard deviation | population standard deviation of the values in X from the start of the workfile/sample to the current observation. Note this calculation involves division by 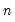 . . |
@cumstdevs(x[,s]) | cumulative sample standard deviation | sample standard deviation of the values in X from the start of the workfile/sample. Note this performs the same calculation as @cumstdev. |
@cumvar(x[,s]) | cumulative variance | population variance of the values in X from the start of the workfile/sample to the current observation. Note this calculation involves division by  . . |
@cumvarp(x[,s]) | cumulative population variance | population variance of the values in X from the start of the workfile/sample to the current observation. Note this performs the same calculation as @cumvar. |
@cumvars(x[,s]) | cumulative sample variance | sample variance of the values in X from the start of the workfile/sample to the current observation. Note this calculation involves division by 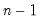 . . |
@cummax(x[,s]) | cumulative maximum | maximum of the values in X from the start of the workfile/sample to the current observation. |
@cummin(x[,s]) | cumulative minimum | minimum of the values in X from the start of the workfile/sample to the current observation. |
@cumsumsq(x[,s]) | cumulative sum-of-squares | sum of squares of the values in X from the start of the workfile/sample to the current observation. |
@cumobs(x[,s]) | cumulative nmber of non-NA observations | the number of non-missing observations in X from the start of the workfile/sample to the current observation. |
@cumnas(x[,s]) | cumulative number of NA observations | the number of missing observations in X from the start of the workfile/sample to the current observation. |
@cumquantile(x,q[,s]) | cumulative quantile | the qth quantile in X computed from the start of the workfile/sample to the current observation. Quantiles are computed using the Cleveland definition. |
@cummedian(x[,s]) | cumulative median | the median of X computed from the end of the workfile/sample to the current observation. |
@cumbsum(x[,s]) | backwards cumulative sum | cumulative sum of the values in X from the end of the workfile/sample. |
@cumbprod(x[,s]) | backwards cumulative product | cumulative product of the values in X from the end of the workfile/sample (note this function could be subject to numerical overflows). |
@cumbmean(x[,s]) | backwards cumulative mean | mean of the values in X from the end of the workfile/sample to the current observation. |
@cumbstdev(x[,s]) | backwards cumulative standard deviation | sample standard deviation of the values in X from the end of the workfile/sample to the current observation. Note this calculation involves division by  . . |
@cumbstdevp(x[,s]) | backwards cumulative population standard deviation | population standard deviation of the values in X from the end of the workfile/sample to the current observation. Note this calculation involves division by 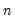 . . |
@cumbstdevs(x[,s]) | backwards cumulative sample standard deviation | sample standard deviation of the values in X from the end of the workfile/sample. Note this performs the same calculation as @cumstdev. |
@cumbvar(x[,s]) | backwards cumulative variance | population variance of the values in X from the end of the workfile/sample to the current observation. Note this calculation involves division by 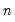 |
@cumbvarp(x[,s]) | backwards cumulative population variance | population variance of the values in X from the end of the workfile/sample to the current observation. Note this performs the same calculation as @cumvar. |
@cumbvars(x[,s]) | backwards cumulative sample variance | sample variance of the values in X from the end of the workfile/sample to the current observation. Note this calculation involves division by 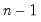 . . |
@cumbmax(x[,s]) | backwards cumulative maximum | maximum of the values in X from the end of the workfile/sample to the current observation. |
@cumbmin(x[,s]) | backwards cumulative minimum | minimum of the values in X from the end of the workfile/sample to the current observation. |
@cumbsumsq(x[,s]) | backwards cumulative sum-of-squares | sum of squares of the values in X from the start of the workfile/sample to the current observation. |
@cumbobs(x[,s]) | backwards cumulative nmber of non-NA observations | the number of non-missing observations in X from the end of the workfile/sample to the current observation. |
@cumbnas(x[,s]) | backwards cumulative nmber of NA observations | the number of missing observations in X from the end of the workfile/sample to the current observation. |
@cumbquantile(x,q[,s]) | backwards cumulative quantile | the qth quantile in X computed from the end of the workfile/sample to the current observation. Quantiles are computed using the Cleveland definition. |
@cumbmedian(x[,s]) | backwards cumulative median | the median of X computed from the end of the workfile/sample to the current observation. |
@dcumdn(x, d[, y, s]) | addition to cumulative negative (below threshold) changes | addition to cumulative process of changes in X from date D, for observations with negative (or below Y threshold) changes. |
@dcumdp(x, d[, y, s]) | addition to cumulative positive (above threshold) changes | addition to cumulative process of changes in X from date D, for observations with positive (or below Y threshold) changes. |
@dcumdz(x, d[, y, s]) | addition cumulative zero (at threshold) changes | addition to cumulative process of changes in X from date D, for observations with positive (or at Y threshold) changes. |