Command Reference : Operator and Function Reference : Descriptive Statistics
  
Descriptive Statistics
These functions compute descriptive statistics for a specified sample, excluding missing values if necessary. The default sample is the current workfile sample. If you are performing these computations on a series and placing the results into a series, you can specify a sample as the last argument of the descriptive statistic function, either as a string (in double quotes) or using the name of a sample object. For example:
series z = @mean(x, "1945m01 1979m12")
or
w = @var(y, s2)
where S2 is the name of a sample object and W and X are series. Note that you may not use a sample argument if the results are assigned into a matrix, vector, or scalar object. For example, the following assignment:
vector(2) a
series x
a(1) = @mean(x, "1945m01 1979m12")
is not valid since the target A(1) is a vector element. To perform this latter computation, you must explicitly set the global sample prior to performing the calculation performing the assignment:
smpl 1945:01 1979:12
a(1) = @mean(x)
To determine the number of observations available for a given series, use the @obs function. Note that where appropriate, EViews will perform casewise exclusion of data with missing values. For example, @cov(x,y) and @cor(x,y) will use only observations for which data on both X and Y are valid.
In the following table, arguments in square brackets [ ] are optional arguments:
• [s]: sample expression in double quotes or name of a sample object. The optional sample argument may only be used if the result is assigned to a series. For @quantile, you must provide the method option argument in order to include the optional sample argument.
If the desired sample expression contains the double quote character, it may be entered using the double quote as an escape character. Thus, if you wish to use the equivalent of,
smpl if name = "Smith"
in your @MEAN function, you should enter the sample condition as:
series y = @mean(x, "if name=""Smith""")
The pairs of double quotes in the sample expression are treated as a single double quote.
 
Function
Name
Description
@cor(x,y[,s])
correlation
the correlation between X and Y.
@cov(x,y[,s])
covariance
the covariance between X and Y (division by ).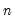
@covp(x,y[,s])
population covariance
the covariance between X and Y (division by ).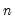
@covs(x,y[,s])
sample covariance
the covariance between X and Y (division by ).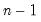
@dupselem(x1[, x2,..., smpl])
duplicate identification
element IDs enumerating the observations within a duplicate group, as determined by @dupsid. The element IDs for any two observations with the same group ID are distinct.
@dupsid(x1[, x2,..., smpl])
duplicate identification
group IDs identifying unique/duplicated observation data, similar to @groupid. The IDs for two observations are identical if and only if the values of series, alphas, or groups s1, s2, etc., are identical for both observations.
@dupsobs(x1[, x2,..., smpl])
duplicate identification
number of occurrences of each observation's group ID as would be assigned by @dupsid. An observation containing a unique combination of values among series, alphas, or groups s1, s2, etc., will therefore have the value one, while any duplicated observation will have a value larger than one.
@gmean(x[,s])
geometric mean
the geometric mean of X. The geometric mean is calculated as the exponential of the sum of the logs of X.
@hmean(x[,s])
harmonic mean
computes the harmonic mean of the values of X. The harmonic mean is calculated as the reciprocal of the mean of the reciprocals of X.
@imax(x)
maximum index
workfile index of the maximum of the values in X for the current sample.
@imin(x)
minimum index
workfile index of the maximum of the values in X for the current sample.
@inner(x,y[,s])
inner product
the inner product of X and Y.
@intercept(x[, s])
intercept
the intercept (or intercepts for panel data) of an OLS regression versus an implicit time trend, as would be used by @detrend. This function is panel aware.
@kurt(x[,s])
kurtosis
kurtosis of values in X.
@mae(x,y[,s])
mean absolute error
the mean of the absolute value of the difference between X and Y.
 
@mape(x,y[,s])
mean absolute percentage error
100 multiplied by the mean of the absolute difference between X and Y, divided by Y.
@max(x[,s])
maximum
maximum of the values in X.
@maxes(x,n[,s])
n-largest numbers
maximum n values in X, arranged largest to smallest, returned in a vector object. Note this function may not be used for series generation.
@mean(x[,s])
mean
average of the values in X.
@median(x[,s])
median
computes the median of the X (uses the average of middle two observations if the number of observations is even).
@min(x[,s])
minimum
minimum of the values in X.
@mins(x,n[,s])
n-smallest numbers
minimum n values in X, arranged smallest to largest, returned in a vector object. Note this function may not be used for series generation.
@mse
mean square error
the mean of the squared difference between X and Y.
@nas(x[,s])
number of NAs
the number of missing observations for X in the current sample.
@pctiles(x[, ties, s])
percentiles
Similar to @ranks, but returns the percentile of each observation within the series.
Equivalent to 100 * @ranks(x, ”a”, ties) / @obs(x).
@prod(x[,s])
product
the product of the elements of X (note this function is prone to numerical overflows).
@obs(x[,s])
number of observations
the number of non-missing observations for X in the current sample.
@quantile(x,q[,m,s])
quantile
the q-th quantile of the series X. m is an optional string argument for specifying the quantile method: “b” (Blom), “r” (Rankit-Cleveland), “o” (Ordinary), “t” (Tukey), “v” (van der Waerden), “g” (Gumbel). The default value is “r”.
@ranks(x[,o,t,s])
ranks
the ranking of each observation in X.
The order of ranking is set using o: “a” (ascending - default) or “d” (descending).
Ties are broken according to the setting of t: “i” (ignore), “f” (first), “l” (last), “a” (average - default), “r” randomize.
If you wish to specify tie-handling options, you must also specify the order option (e.g. ‘@ranks(x, “a”, “i”)’).
@rmse(x,y[,s])
root mean square error
the square root of the mean of the squared difference between X and Y.
@skew(x[,s])
skewness
skewness of values in X.
@smape(x,y[,s])
symmetric mean absolute percentage error
200 multiplied by the mean of the absolute difference between X and Y divided by the sum of the absolute values of X and Y.
@stdev(x[,s])
standard deviation
square root of the unbiased sample variance (sum-of-squared residuals divided by ).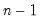
@stdevp(x[,s])
population standard deviation
square root of the population variance (sum-of-squared residuals divided by ).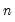
@stdevs(x[,s])
sample standard deviation
square root of the unbiased sample variance. Note this is the same calculation as @stdev.
@stdize(x[, smpl])
standardize (for sample)
Returns a copy of series scaled and translated to have a mean of zero and a sample standard deviation of one.
@stdizep(x[, smpl])
standardize (for population)
Returns a copy of series scaled and translated to have a mean of zero and a population standard deviation of one.
@sum(x[,s])
sum
the sum of X.
@sumsq(x[,s])
sum-of-squares
sum of the squares of X.
@theil(x,y[,s])
Theil inequality coefficient
the root mean square error divided by the sum of the square roots of the means of X squared and Y squared.
@trendcoef(x[, s])
trend coefficient
the slope of an OLS regression versus an implicit time trend, as would be used by @detrend. This function is panel aware.
@trmean(x, p[, s])
trimmed mean
Returns the p-percent trimmed mean, i.e. the mean of after the p-percent largest and smallest values have been removed.
@var(x[,s])
variance
variance of the values in X (division by ).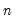
@varp(x[,s])
population variance
variance of the values in X. Note this is the same calculation as @var.
@vars(x[,s])
sample variance
sample variance of the values in X (division by 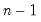).