Name | Function | Description |
@columns(g) | number of columns. | returns the number of columns in G. Note this is the same as “G.@count”, and will return the same number for every row. |
@rnas(g) | row-wise number of NAs. | the number of missing observations in the rows of G. |
@robs(g) | row-wise number of non-NAs. | the number of non-missing observations in the rows of G. |
@rvalcount(g,v) | row-wise count of observations matching v. | the number of observations with a value equal to v in the rows of G. Note v can be a scalar or a series |
@rsum(g) | row-wise sum. | the sum of the rows of G. |
@rmean(g) | row-wise mean. | the mean of the rows of G. |
@rmedian(g) | row-wise median | the median of the rows of G. |
@rprod(g) | row-wise product | the product of the rows of G. Beware overflow. |
@rquantile(g,q) | row-wise quantile, where q is the quantile | the quantile of the rows of G. The Cleveland quantile definition is used. |
@rstdev(g) | row-wise standard deviation. | the sample standard deviation of the rows of G. Note division is by 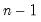 . . |
@rstdevp(g) | row-wise population standard deviation. | the population standard deviation of the rows of G. Note division is by 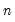 . . |
@rstdevs(g) | row-wise sample standard deviation. | the sample standard deviation of the rows of G. Note division is by 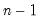 , and this calculation is the same as @rstdev. , and this calculation is the same as @rstdev. |
@rvar(g) | row-wise variance. | the population variance of the rows of G. Note division is by 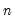 . . |
@rvarp(g) | row-wise population variance | the population variance of the rows of G. Note division is by 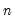 , and this calculation is the same as @rvar. , and this calculation is the same as @rvar. |
@rvars(g) | row-wise sample variance. | the sample variance of the rows of G. Note division is by 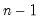 . . |
@rsumsq(g) | row-wise sum-of-squares. | the sum of the squares of the rows of G. |
@rfirst(g) | row-wise first non-NA value. | the value of the first non-missing observation in the rows of G. |
@rifirst(g) | row-wise first non-NA index. | the index (i.e., column number) of the first non-missing observation in the rows of G. |
@rilast(g) | row-wise last non-NA index. | the index (i.e., column number) of the last non-missing observation in the rows of G. |
@rimax(g) | row-wise maximum index. | the index (i.e., column number) of the maximum observation in the rows of G. In the case of ties, the first matching index is given. |
@rimin(g) | row-wise minimum index. | the index (i.e., column number) of the minimum observation in the rows of G. In the case of ties, the first matching index is given. |
@rlast(g) | row-wise last non-NA value. | the value of the last non-missing observation in the rows of G |
@rmax(g) | row-wise maximum value. | the value of the maximum observation in the rows of G. |
@rmin(g) | row-wise minimum value. | the value of the minimum observation in the rows of G. |