Scale rows or columns of matrix.
Syntax: @scale(m, v[,p])
m: matrix, sym
v: vector
p: (optional) number
Return: matrix, sym
Scale the rows or columns of a matrix, or the rows and columns of a sym matrix.
• If m is a matrix and v is a vector, the i-th row of m will be scaled by the i-th element of v, optionally raised to the power p (row scaling). The length v must equal the number of rows of m.
• If m is a matrix and v is a rowvector, the i-th column of m will be scaled by the i-th element of v, optionally raised to the power p (column scaling). The length v must equal the number of columns of m.
• If m is a sym object, then v may either be a vector or a rowvector. The (i,j)-th element of m will be scaled by both the i-th and j-th elements of v (row and column scaling). The length v must equal the number of rows (and columns) of m.
Let M be the matrix object, V be the vector or rowvector, and
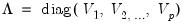
be the diagonal matrix formed from the elements of V. Then
@scale(m, v, p) returns:
• 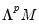
, if M is a matrix and V is a vector.
• 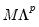
, if M is a matrix and V is a rowvector.
• 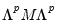
, if M is a sym matrix.
Examples
sym covmat = @cov(grp1)
vector vars = @getmaindiagonal(covmat)
sym corrmat = @scale(covmat, vars, -0.5)
computes the covariance matrix for the series in the group object GRP1, extracts the variances to a vector VARS, then uses VARS to obtain a correlation matrix from the covariance matrix.
matrix covmat1 = covmat
matrix rowscaled = @scale(covmat, vars, -0.5)
matrix colscaled = @scale(covmat, @transpose(vars), -0.5)
sym corrmat1 = colscaled
performs the same scaling in multiple steps. Note that the COLSCALED matrix is square and symmetric, but not a sym object.
Cross-references
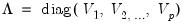 be the diagonal matrix formed from the elements of V. Then @scale(m, v, p) returns:
be the diagonal matrix formed from the elements of V. Then @scale(m, v, p) returns: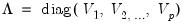 be the diagonal matrix formed from the elements of V. Then @scale(m, v, p) returns:
be the diagonal matrix formed from the elements of V. Then @scale(m, v, p) returns: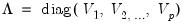 be the diagonal matrix formed from the elements of V. Then @scale(m, v, p) returns:
be the diagonal matrix formed from the elements of V. Then @scale(m, v, p) returns: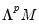 , if M is a matrix and V is a vector.
, if M is a matrix and V is a vector.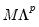 , if M is a matrix and V is a rowvector.
, if M is a matrix and V is a rowvector.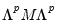 , if M is a sym matrix.
, if M is a sym matrix.