Singular value decomposition (economy) of matrix
Syntax: @svd(m1, v1, m2)
m1: matrix, sym
v1: vector
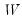
m2: matrix, sym
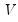
Return: matrix
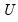
Performs an “economy” or “thin” singular value decomposition of the matrix m1, generating truncated results when m1 is not square (exploiting the reduced maximum rank of a non-square matrix).
The matrix
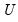
is returned by the function, the vector
v1 will be filled (resized if necessary) with the singular values and the matrix
m2 will be assigned (resized if necessary) the other matrix,
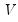
, of the decomposition. The singular value decomposition satisfies:
where
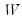
is a diagonal matrix with the singular values along the diagonal. Singular values close to zero indicate that the matrix may not be of full rank. See the
@rank function for a related discussion.
Let r be the number of rows of m1 and s be the number of columns of m1 so that m1 has at most t = min(r, s) distinct singular values. Then
• m2 will be s-by-t
• v1 will be t-by-1
• 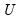
will have dimensions
r-by-
t Examples
matrix x = @mnrnd(5, 7)
vector w
matrix v
matrix u = @svd(x, w, v)
performs the thin SVD of the matrix X. U is
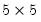
, W is a 5 element vector containing the singular values, and V is a
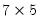
matrix.
Alternately, if the rank is less than the number of rows,
matrix x = @mnrnd(7, 5)
matrix u = @svd(x, w, v)
U is
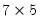
, W is a 5 element vector containing the singular values, and V is a
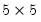
matrix.
The following demonstrate the properties of the decomposition:
sym i1 = @inner(u)
sym i2 = @inner(v)
matrix x1 = u * @makediagonal(w) * v.@t()
where I1 and I2 and the identity matrix, and X1 is equal to X.
Cross-references
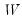
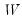
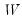
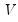
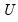
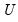 is returned by the function, the vector v1 will be filled (resized if necessary) with the singular values and the matrix m2 will be assigned (resized if necessary) the other matrix,
is returned by the function, the vector v1 will be filled (resized if necessary) with the singular values and the matrix m2 will be assigned (resized if necessary) the other matrix, 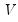 , of the decomposition. The singular value decomposition satisfies:
, of the decomposition. The singular value decomposition satisfies: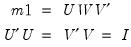
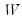 is a diagonal matrix with the singular values along the diagonal. Singular values close to zero indicate that the matrix may not be of full rank. See the
@rank function for a related discussion.
is a diagonal matrix with the singular values along the diagonal. Singular values close to zero indicate that the matrix may not be of full rank. See the
@rank function for a related discussion. 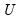 will have dimensions r-by-t
will have dimensions r-by-t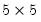 , W is a 5 element vector containing the singular values, and V is a
, W is a 5 element vector containing the singular values, and V is a 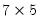 matrix.
matrix.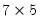 , W is a 5 element vector containing the singular values, and V is a
, W is a 5 element vector containing the singular values, and V is a 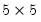 matrix.
matrix.