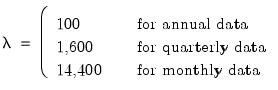Technically, the Hodrick-Prescott (HP) filter is a two-sided linear filter that computes the smoothed series 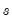 of
of 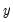 by minimizing the variance of
by minimizing the variance of 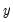 around
around 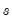 , subject to a penalty that constrains the second difference of
, subject to a penalty that constrains the second difference of 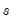 . That is, the HP filter chooses
. That is, the HP filter chooses 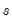 to minimize:
to minimize:
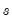 of
of 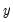 by minimizing the variance of
by minimizing the variance of 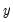 around
around 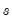 , subject to a penalty that constrains the second difference of
, subject to a penalty that constrains the second difference of 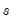 . That is, the HP filter chooses
. That is, the HP filter chooses 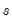 to minimize:
to minimize: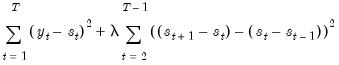
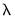 controls the smoothness of the series
controls the smoothness of the series 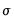 . The larger the
. The larger the 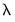 , the smoother the
, the smoother the 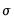 . As
. As 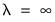 ,
, 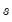 approaches a linear trend.
approaches a linear trend.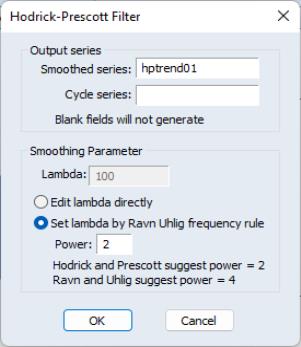
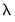 . You may specify the parameter using the frequency power rule of Ravn and Uhlig (2002) (the number of periods per year divided by 4, raised to a power, and multiplied by 1600), or you may specify
. You may specify the parameter using the frequency power rule of Ravn and Uhlig (2002) (the number of periods per year divided by 4, raised to a power, and multiplied by 1600), or you may specify 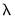 directly. The default is to use a power rule of 2, yielding the original Hodrick and Prescott values for
directly. The default is to use a power rule of 2, yielding the original Hodrick and Prescott values for 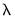 :
: