Perform Error-Trend-Season (ETS) exponential smoothing.
The ets procedure forecasts a series using the ETS model framework with state-space based likelihood calculations, support for model selection, and calculation of forecast standard errors.
The ETS framework defines an extended class of exponential smoothing models, including the standard exponential smoothing models (e.g., Holt and Holt-Winters additive and multiplicative models).
Syntax
series_name.ets(options) smooth_name
You should enter the ets keyword followed by options and then the a name for the smoothed output series. You can specify the smoothing method (the default setting is additive error, no trend, no seasonality) and the smoothing options in the parenthesis.
Options
Forecast sample options
The forecast sample will start at the observation immediately after the estimation sample (the current workfile sample). The forecast endpoint is given by either:
forclen=int | Number of periods to forecast. |
forc="date" | Specify the date of the forecast end point. |
One of these options is required.
General
prompt | Force the dialog to appear from within a program. |
p | Print the view. |
Model specification
e=arg (default = “a”) | Set error type: “a” (additive), “m” (multiplicative), “e” (auto). |
t=arg (default = “n”) | Set trend type. key can be: “n” (none), “a” (additive), “m” (multiplicative), “ad” (additive dampened), “md” (multiplicative dampened), “e” (auto). |
s=arg (default = “n”) | Set season type. key can be: “n” (none), “a”(additive), “m” (multiplicative), “e” (auto). |
modsel=arg (default= “aic”) | Model selection method: “aic” (Akaike information criterion), “bic” (Bayesian information criterion/Schwartz criterion), “hq” (Hannan-Quinn information criterion), “amse” (average mean squared errors). |
alpha=arg | Specify fixed value for level parameter 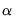 . |
beta=arg | Specify fixed value for trend parameter 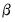 in models with trend. |
gamma=arg | Specify fixed value for seasonal parameter 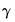 in models with a seasonal component. |
phi=arg | Specify fixed value for dampening parameter 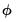 in models with dampened trends. |
nomult | Do not allow multiplicative trend or seasonal terms. Only applies if the t=e or s=e options are set. |
Optimization options
amse | Set Average Mean Square Error (AMSE) as the objective function (The default is log-likelihood as the objective function). |
namse=integer | Specify the AMSE length—the number of observations over which to calculate AMSE if “amse” is selected. |
c=number | Set the convergence criteria. |
m=integer | Set the maximum number of iterations. |
ustart | Employ user-supplied starting values (taken from the C vector in the workfile). |
noi | Do not optimize the initial state values (fix at their starting values). |
Output options
dgraph=arg | Include a decomposition graph for each specified element. arg may be composed of any of the following elements: “f” (forecast), “l” (level), “t” (trend), “s” (season). |
dgopt=arg (default =“m”) | Format for display of decomposition graph: “m” (multiple graph), “s” (single graph) |
graph=arg | Include a comparison graph in the output for each specified element (if model selection is employed). arg may be composed of any of the following elements: “c” (forecast comparison) and “l” (likelihood comparison). |
table=arg | Include a comparison table in the output (if model selection is employed). arg may be composed of any of the following elements: “c” (forecast comparison) and “l” (likelihood comparison). |
level=name | Save the level component as a separate series in the workfile. |
trend=name | Save the trend component as a separate series in the workfile (if applicable). |
season=name | Save the seasonal component as a separate series in the workfile (if applicable). |
Examples
sales.ets(e=a, t=n, s=a)sales_f
smooths the series SALES using the an ANN (additive error, no trend, no seasonal) model and creates the smoothed series named “SALES_F”.
tb3.ets(e=e, t=e, s=n) tb3_smooth
will smooth TB3, automatically selecting the best smoothing model amongst the different Error and Trend specifications (the Seasonal specification is set at none).
sales.ets(e=a, t=a, s=a, dgopt=m, dgraph=flts)
will smooth the series SALES using the an AAA (additive error, additive trend, additive seasonal) model and display the output in a spool object which contains the actual and decomposition series (i.e., forecast, trend, level, and seasonal series) in multiple graphs.
sales.ets(e=a, t=a, s=a, level=level1, trend=trend1, season=season1, dgopt=s, dgraph=flts)
will smooth the series SALES using the an AAA (additive error, additive trend, additive seasonal) model, create the decomposition series named level, trend, and season series as level1, trend1, and season1, respectively, and display a spool object which contains the actual and decomposition graphs in a single graph.
tb3.ets(e=e, t=e, s=e, graph=cl)
will find out the best model amongst the different Error, Trend, and Seasonal specifications and present the estimation results in a spool object which contains the graphs with forecast and likelihood comparison graphs between all available models.
tb3.ets(e=a, t=e, s=e, amse, table=cl)
will search for the best model using average mean square errors calculations and display the estimation results in a spool object with forecast and likelihood comparison tables.
Cross-references
See
“Exponential Smoothing” for a discussion of exponential smoothing methods.
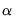 .
.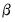 in models with trend.
in models with trend.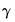 in models with a seasonal component.
in models with a seasonal component.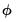 in models with dampened trends.
in models with dampened trends.