Background
A system is a group of equations containing unknown parameters. Systems can be estimated using a number of multivariate techniques that take into account the interdependencies among the equations in the system.
The general form of a system is:
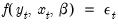 | (43.1) |
where
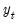
is a vector of endogenous variables,
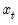
is a vector of exogenous variables, and
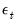
is a vector of possibly serially correlated disturbances. The task of estimation is to find estimates of the vector of parameters
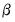
.
EViews provides you with a number of methods of estimating the parameters of the system. One approach is to estimate each equation in the system separately, using one of the single equation methods described earlier in this manual. A second approach is to estimate, simultaneously, the complete set of parameters of the equations in the system. The simultaneous approach allows you to place constraints on coefficients across equations and to employ techniques that account for correlation in the residuals across equations.
While there are important advantages to using a system to estimate your parameters, they do not come without cost. Most importantly, if you misspecify one of the equations in the system and estimate your parameters using single equation methods, only the misspecified equation will be poorly estimated. If you employ system estimation techniques, the poor estimates for the misspecification equation may “contaminate” estimates for other equations.
At this point, we take care to distinguish between systems of equations and models. A model is a group of known equations describing endogenous variables. Models are used to solve for values of the endogenous variables, given information on other variables in the model.
Systems and models often work together quite closely. You might estimate the parameters of a system of equations, and then create a model in order to forecast or simulate values of the endogenous variables in the system. We discuss this process in greater detail in
“Models”.
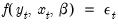
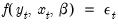
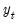 is a vector of endogenous variables,
is a vector of endogenous variables, 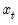 is a vector of exogenous variables, and
is a vector of exogenous variables, and 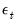 is a vector of possibly serially correlated disturbances. The task of estimation is to find estimates of the vector of parameters
is a vector of possibly serially correlated disturbances. The task of estimation is to find estimates of the vector of parameters 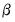 .
.