The “name=” option stores the following matrix. Let the VAR have 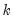 endogenous variables. Then the stored matrix will have dimension
endogenous variables. Then the stored matrix will have dimension 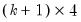 . The first
. The first 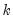 rows contain statistics for each orthogonal component, where the first column contains the third moments, the second column contains the
rows contain statistics for each orthogonal component, where the first column contains the third moments, the second column contains the 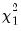 statistics for the third moments, the third column contains the fourth moments, and the fourth column holds the
statistics for the third moments, the third column contains the fourth moments, and the fourth column holds the 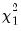 statistics for the fourth moments. The sum of the second and fourth columns are the Jarque-Bera statistics reported in the last output table.
statistics for the fourth moments. The sum of the second and fourth columns are the Jarque-Bera statistics reported in the last output table.
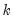 endogenous variables. Then the stored matrix will have dimension
endogenous variables. Then the stored matrix will have dimension 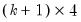 . The first
. The first 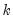 rows contain statistics for each orthogonal component, where the first column contains the third moments, the second column contains the
rows contain statistics for each orthogonal component, where the first column contains the third moments, the second column contains the 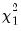 statistics for the third moments, the third column contains the fourth moments, and the fourth column holds the
statistics for the third moments, the third column contains the fourth moments, and the fourth column holds the 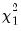 statistics for the fourth moments. The sum of the second and fourth columns are the Jarque-Bera statistics reported in the last output table.
statistics for the fourth moments. The sum of the second and fourth columns are the Jarque-Bera statistics reported in the last output table.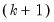 row is simply the sum of all the rows above in the corresponding column and are the
row is simply the sum of all the rows above in the corresponding column and are the 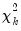 statistics for the joint skewness and kurtosis tests, respectively. These joint skewness and kurtosis statistics add up to the joint Jarque-Bera statistic reported in the output table, except for the “factor=cov” option. When this option is set, the joint Jarque-Bera statistic includes all cross moments (in addition to the pure third and fourth moments). The overall Jarque-Bera statistic for this statistic is stored in the first column of the
statistics for the joint skewness and kurtosis tests, respectively. These joint skewness and kurtosis statistics add up to the joint Jarque-Bera statistic reported in the output table, except for the “factor=cov” option. When this option is set, the joint Jarque-Bera statistic includes all cross moments (in addition to the pure third and fourth moments). The overall Jarque-Bera statistic for this statistic is stored in the first column of the 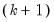 row (which will be a missing value for all other options).
row (which will be a missing value for all other options).