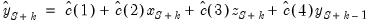Forecasts with Lagged Dependent Variables
Forecasting is complicated by the presence of lagged dependent variables on the right-hand side of the equation. For example, we can augment the earlier specification to include the first lag of Y:
y c x z y(-1)
and click on the button and fill out the series names in the dialog as above. There is some question, however, as to how we should evaluate the lagged value of Y that appears on the right-hand side of the equation. There are two possibilities: dynamic forecasting and static forecasting.
Dynamic Forecasting
If you select dynamic forecasting, EViews will perform a multi-step forecast of Y, beginning at the start of the forecast sample. For our single lag specification above:
• The initial observation in the forecast sample will use the actual value of lagged Y. Thus, if
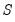
is the first observation in the forecast sample, EViews will compute:
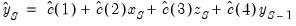 | (25.6) |
where
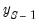
is the value of the lagged endogenous variable in the period prior to the start of the forecast sample. This is the one-step ahead forecast.
• Forecasts for subsequent observations will use the previously forecasted values of Y:
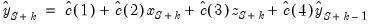 | (25.7) |
• These forecasts may differ significantly from the one-step ahead forecasts.
If there are additional lags of Y in the estimating equation, the above algorithm is modified to account for the non-availability of lagged forecasted values in the additional period. For example, if there are three lags of Y in the equation:
• The first observation (
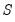
) uses the actual values for all three lags,
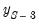
,
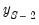
, and
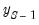
.
• The second observation (
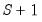
) uses actual values for
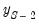
and,
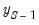
and the forecasted value
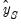
of the first lag of
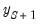
.
• The third observation (
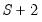
) will use the actual values for
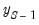
, and forecasted values
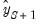
and
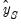
for the first and second lags of
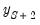
.
• All subsequent observations will use the forecasted values for all three lags.
The selection of the start of the forecast sample is very important for dynamic forecasting. The dynamic forecasts are true multi-step forecasts (from the start of the forecast sample), since they use the recursively computed forecast of the lagged value of the dependent variable. These forecasts may be interpreted as the forecasts for subsequent periods that would be computed using information available at the start of the forecast sample.
Dynamic forecasting requires that data for the exogenous variables be available for every observation in the forecast sample, and that values for any lagged dependent variables be observed at the start of the forecast sample (in our example,
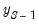
, but more generally, any lags of
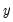
). If necessary, the forecast sample will be adjusted.
Any missing values for the explanatory variables will generate an NA for that observation and in all subsequent observations, via the dynamic forecasts of the lagged dependent variable.
Lastly, we note that for non-linear dynamic forecasting, EViews produces what Tong and Lim (1980) term the “eventual forecasting function” in which the lagged forecasted values are substituted recursively into the one-step ahead function. This approach differs from the simulation based approaches to multi-step forecasting which employs stochastic simulation. If you wish to obtain the latter forecasts, click on the checkbox and enter the number of and as desired.
Static Forecasting
Static forecasting performs a series of one-step ahead forecasts of the dependent variable:
• For each observation in the forecast sample, EViews computes:
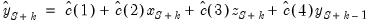 | (25.8) |
always using the actual value of the lagged endogenous variable.
Static forecasting requires that data for both the exogenous and any lagged endogenous variables be observed for every observation in the forecast sample. As above, EViews will, if necessary, adjust the forecast sample to account for pre-sample lagged variables. If the data are not available for any period, the forecasted value for that observation will be an NA. The presence of a forecasted value of NA does not have any impact on forecasts for subsequent observations.
A Comparison of Dynamic and Static Forecasting
Both methods will always yield identical results in the first period of a multi-period forecast. Thus, two forecast series, one dynamic and the other static, should be identical for the first observation in the forecast sample.
The two methods will differ for subsequent periods only if there are lagged dependent variables or ARMA terms.
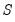 is the first observation in the forecast sample, EViews will compute:
is the first observation in the forecast sample, EViews will compute: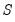 is the first observation in the forecast sample, EViews will compute:
is the first observation in the forecast sample, EViews will compute: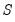 is the first observation in the forecast sample, EViews will compute:
is the first observation in the forecast sample, EViews will compute: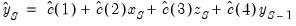
 is the value of the lagged endogenous variable in the period prior to the start of the forecast sample. This is the one-step ahead forecast.
is the value of the lagged endogenous variable in the period prior to the start of the forecast sample. This is the one-step ahead forecast.
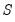 ) uses the actual values for all three lags,
) uses the actual values for all three lags, 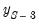 ,
, 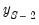 , and
, and 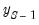 .
.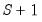 ) uses actual values for
) uses actual values for 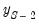 and,
and, 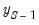 and the forecasted value
and the forecasted value 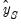 of the first lag of
of the first lag of 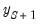 .
.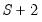 ) will use the actual values for
) will use the actual values for 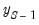 , and forecasted values
, and forecasted values 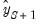 and
and 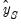 for the first and second lags of
for the first and second lags of 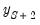 .
.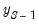 , but more generally, any lags of
, but more generally, any lags of 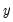 ). If necessary, the forecast sample will be adjusted.
). If necessary, the forecast sample will be adjusted.