Stepwise Least Squares Regression
EViews allows you to perform automatic variable selection using stepwise regression. Stepwise regression allows some or all of the variables in a standard linear multivariate regression to be chosen automatically, using various statistical criteria, from a set of variables.
There is a fairly large literature describing the benefits and the pitfalls of stepwise regression. Without making any recommendations ourselves, we refer the user to Derksen and Keselman (1992), Roecker (1991), Hurvich and Tsai (1990).
Stepwise Least Squares Estimation in EViews
To perform a Stepwise selection procedure (STEPLS) in EViews select , or press from the toolbar of an existing equation. From the Equation Specification dialog choose Method: STEPLS - Stepwise Least Squares. EViews will display the following dialog:
The Specification page allows you to provide the basic STEPLS regression specification. In the upper edit field you should first specify the dependent variable followed by the always included variables you wish to use in the final regression. Note that the STEPLS equation must be specified by list.
You should enter a list of variables to be used as the set of potentially included variables in the second edit field.
Next, you may use the tab to control the stepwise estimation method.
The portion of the page is used to specify the STEPLS method.
By default, EViews will estimate the stepwise specification using the Stepwise-Forwards method. To change the basic method, change the Selection Method dropdown menu; the dropdown allows you to choose between: , , , and .
The other items on this dialog tab will change depending upon which method you choose. For the and methods you may specify the direction of the method using the Forwards and Backwards radio buttons. These two methods allow you to provide a Stopping Criteria using either a p-value or t-statistic tolerance for adding or removing variables. You may also choose to stop the procedures once they have added or removed a specified number of regressors by selecting the Use number of regressors option and providing a number of the corresponding edit field.
You may also set the maximum number of steps taken by the procedure. To set the maximum number of additions to the model, change the Forwards steps, and to set the maximum number of removals, change the Backwards steps. You may also set the total number of additions and removals. In general it is best to leave these numbers at a high value. Note, however, that the routines have the potential to repetitively add and remove the same variables, and by setting the maximum number of steps you can mitigate this behavior.
The method lets you choose whether you wish to use or , and choose the number of additional variables to be selected. The method simply prompts you to provide the number of additional variables. By default both of these procedures have the number of additional variables set to one. In both cases this merely chooses the single variable that will lead to the largest increase in R-squared.
For additional discussion, see
“Selection Methods”.
Lastly, each of the methods lets you choose a
Weight series to perform weighted least squares estimation. Simply check the option, then enter the name of the weight series in the edit field. See
“Weighted Least Squares” for details.
Example
As an example we use the following code to generate a workfile with 40 independent variables (X1–X40), and a dependent variable, Y, which is a linear combination of a constant, variables X11–X15, and a normally distributed random error term.
create u 100
rndseed 1
group xs
for !i=1 to 40
series x!i=nrnd
%name="x"+@str(!i)
xs.add {%name}
next
series y = nrnd + 3
for !i=11 to 15
y = y + !i*x{!i}
next
The 40 independent variables are contained in the group XS.
Given this data we can use a forwards stepwise routine to choose the “best” 5 regressors, after the constant, from the group of 40 in XS. We do this by entering “Y C” in the first Specification box of the estimation dialog, and “XS” in the List of search regressors box. In the Stopping Criteria section of the Options tab we check Use Number of Regressors, and enter “5” as the number of regressors. Estimating this specification yields the results:
The top portion of the output shows the equation specification and information about the stepwise method. The next section shows the final estimated specification along with coefficient estimates, standard errors and t-statistics, and p-values. Note that the stepwise routine chose the “correct” five regressors, X11–X15. The bottom portion of the output shows a summary of the steps taken by the selection method. Specifications with a large number of steps may show only a brief summary.
Selection Methods
EViews allows you to specify variables to be included as regressors along with a set of variables from which the selection procedure will choose additional regressors. The first set of variables are termed the “always included” variables, and the latter are the set of potential “added variables”. EViews supports several procedures for selecting the added variables.
Uni-directional-Forwards
The Uni-directional-Forwards method uses either a lowest p-value or largest t-statistic criterion for adding variables.
The method begins with no added regressors. If using the p-value criterion, we select the variable that would have the lowest p-value were it added to the regression. If the p-value is lower than the specified stopping criteria, the variable is added. The selection continues by selecting the variable with the next lowest p-value, given the inclusion of the first variable. The procedure stops when the lowest p-value of the variables not yet included is greater than the specified forwards stopping criterion, or the number of forward steps or number of added regressors reach the optional user specified limits.
If using the largest t-statistic criterion, the same variables are selected, but the stopping criterion is specified in terms of the statistic value instead of the p-value.
Uni-directional-Backwards
The Uni-directional-Backwards method is analogous to the Uni-directional-Forwards method, but begins with all possible added variables included, and then removes the variable with the highest p-value. The procedure continues by removing the variable with the next highest p-value, given that the first variable has already been removed. This process continues until the highest p-value is less than the specified backwards stopping criteria, or the number of backward steps or number of added regressors reach the optional user specified limits.
The largest t-statistic may be used in place of the lowest p-value as a selection criterion.
Stepwise-Forwards
The Stepwise-Forwards method is a combination of the Uni-directional-Forwards and Backwards methods. Stepwise-Forwards begins with no additional regressors in the regression, then adds the variable with the lowest p-value. The variable with the next lowest p-value given that the first variable has already been chosen, is then added. Next both of the added variables are checked against the backwards p-value criterion. Any variable whose p-value is higher than the criterion is removed.
Once the removal step has been performed, the next variable is added. At this, and each successive addition to the model, all the previously added variables are checked against the backwards criterion and possibly removed. The Stepwise-Forwards routine ends when the lowest p-value of the variables not yet included is greater than the specified forwards stopping criteria (or the number of forwards and backwards steps or the number of added regressors has reached the corresponding optional user specified limit).
You may elect to use the largest t-statistic in place of the lowest p-value as the selection criterion.
Stepwise-Backwards
The Stepwise-Backwards procedure reverses the Stepwise-Forwards method. All possible added variables are first included in the model. The variable with the highest p-value is first removed. The variable with the next highest p-value, given the removal of the first variable, is also removed. Next both of the removed variables are checked against the forwards p-value criterion. Any variable whose p-value is lower than the criterion is added back in to the model.
Once the addition step has been performed, the next variable is removed. This process continues where at each successive removal from the model, all the previously removed variables are checked against the forwards criterion and potentially re-added. The Stepwise-Backwards routine ends when the largest p-value of the variables inside the model is less than the specified backwards stopping criterion, or the number of forwards and backwards steps or number of regressors reaches the corresponding optional user specified limit.
The largest t-statistic may be used in place of the lowest p-value as a selection criterion.
Swapwise-Max R-Squared Increment
The Swapwise method starts with no additional regressors in the model. The procedure starts by adding the variable which maximizes the resulting regression R-squared. The variable that leads to the largest increase in R-squared is then added. Next each of the two variables that have been added as regressors are compared individually with all variables not included in the model, calculating whether the R-squared could be improved by swapping the “inside” with an “outside” variable. If such an improvement exists then the “inside” variable is replaced by the “outside” variable. If there exists more than one swap that would improve the R-squared, the swap that yields the largest increase is made.
Once a swap has been made the comparison process starts again. Once all comparisons and possible swaps are made, a third variable is added, with the variable chosen to produce the largest increase in R-squared. The three variables inside the model are then compared with all the variables outside the model and any R-squared increasing swaps are made. This process continues until the number of variables added to the model reaches the user-specified limit.
Swapwise-Min R-Squared Increment
The Min R-squared Swapwise method is very similar to the Max R-squared method. The difference lies in the swapping procedure. Whereas the Max R-squared swaps the variables that would lead to the largest increase in R-squared, the Min R-squared method makes a swap based on the smallest increase. This can lead to a more lengthy selection process, with a larger number of combinations of variables compared.
Combinatorial
For a given number of added variables, the Combinatorial method evaluates every possible combination of added variables, and selects the combination that leads to the largest R-squared in a regression using the added and always included variables as regressors. This method is more thorough than the previous methods, since those methods do not compare every possible combination of variables, and obviously requires additional computation. With large numbers of potential added variables, the Combinatorial approach can take a very long time to complete.
Lasso selection
If the Lasso selection method is chosen, then ENET estimation is applied with
and variable weights equal to zero for the always included variables. Variables with estimated coefficients equal to zero are left out of the subsequent least squares estimation. All of the options available for ENET are also available for Lasso selection with the exception of the @VW tag. Caution should be used when applying Lasso selection to models with highly collinear variables, as this method will select one variable at random from a group of such variables.
Issues with Stepwise Estimation
The set of search variables may contain variables that are linear combinations of other variables in the regression (either in the always included list, or in the search set). EViews will drop those variables from the search set. In a case where two or more of the search variables are collinear, EViews will select the variable listed first in the list of search variables.
Following the Stepwise selection process, EViews reports the results of the final regression, i.e. the regression of the always-included and the selected variables on the dependent variable. In some cases the sample used in this equation may not coincide with the regression that was used during the selection process. This will occur if some of the omitted search variables have missing values for some observations that do not have missing values in the final regression. In such cases EViews will print a warning in the regression output.
The p-values listed in the final regression output and all subsequent testing procedures do not account for the regressions that were run during the selection process. One should take care to interpret results accordingly.
Invalid inference is but one of the reasons that stepwise regression and other variable selection methods have a large number of critics amongst statisticians. Other problems include an upwardly biased final R-squared, possibly upwardly biased coefficient estimates, and narrow confidence intervals. It is also often pointed out that the selection methods themselves use statistics that do not account for the selection process.
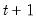
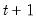
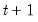
 and variable weights equal to zero for the always included variables. Variables with estimated coefficients equal to zero are left out of the subsequent least squares estimation. All of the options available for ENET are also available for Lasso selection with the exception of the @VW tag. Caution should be used when applying Lasso selection to models with highly collinear variables, as this method will select one variable at random from a group of such variables.
and variable weights equal to zero for the always included variables. Variables with estimated coefficients equal to zero are left out of the subsequent least squares estimation. All of the options available for ENET are also available for Lasso selection with the exception of the @VW tag. Caution should be used when applying Lasso selection to models with highly collinear variables, as this method will select one variable at random from a group of such variables.