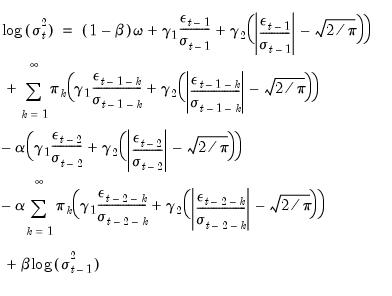Additional ARCH Models
In addition to the standard GARCH specification, EViews has the flexibility to estimate several other variance models. These include IGARCH, TARCH, EGARCH, PARCH, and component GARCH. For each of these models, the user has the ability to choose the order, if any, of asymmetry.
The Integrated GARCH (IGARCH) Model
If one restricts the parameters of the GARCH model to sum to one and drop the constant term
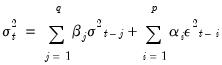 | (27.19) |
such that
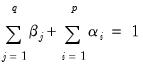 | (27.20) |
then we have an integrated GARCH. This model was originally described in Engle and Bollerslev (1986). To estimate this model, select IGARCH in the Restrictions drop-down menu for the GARCH/TARCH model.
The Threshold GARCH (TARCH) Model
TARCH or Threshold ARCH and Threshold GARCH were introduced independently by Zakoïan (1994) and Glosten, Jaganathan, and Runkle (1993). The generalized specification for the conditional variance is given by:
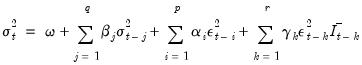 | (27.21) |
where
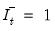
if
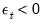
and 0 otherwise.
In this model, good news,
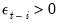
, and bad news.
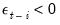
, have differential effects on the conditional variance; good news has an impact of
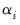
, while bad news has an impact of
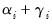
. If
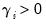
, bad news increases volatility, and we say that there is a
leverage effect for the
i-th order. If
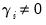
, the news impact is asymmetric.
Note that GARCH is a special case of the TARCH model where the threshold term is set to zero. To estimate a TARCH model, specify your GARCH model with ARCH and GARCH order and then change the to the desired value.
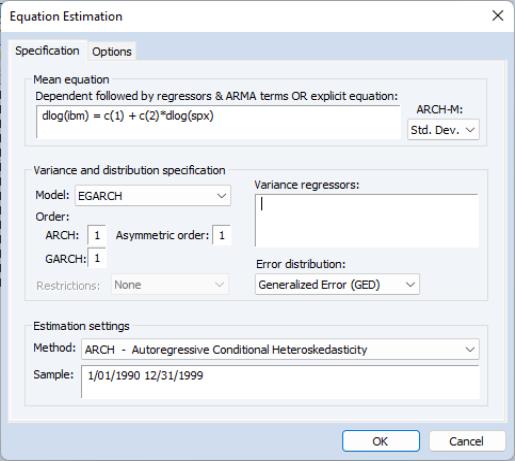
The Exponential GARCH (EGARCH) Model
The EGARCH or Exponential GARCH model was proposed by Nelson (1991). The specification for the conditional variance is:
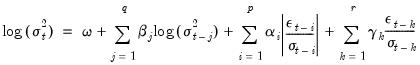 | (27.22) |
Note that the left-hand side is the
log of the conditional variance. This implies that the leverage effect is exponential, rather than quadratic, and that forecasts of the conditional variance are guaranteed to be nonnegative. The presence of leverage effects can be tested by the hypothesis that
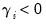
. The impact is asymmetric if
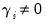
.
There are two differences between the EViews specification of the EGARCH model and the original Nelson model. First, Nelson assumes that the
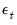
follows a Generalized Error Distribution (GED), while EViews offers you a choice of normal, Student’s
t-distribution, or GED. Second, Nelson's specification for the log conditional variance is a restricted version of:
which is an alternative parameterization of the specification above. Estimating the latter model will yield identical estimates to those reported by EViews except for the intercept term
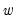
, which will differ in a manner that depends upon the distributional assumption and the order
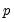
. For example, in a
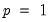
model with a normal distribution, the difference will be
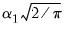
.
To estimate an EGARCH model, simply select the in the model specification dropdown menu and enter the orders for the , and the .
Notice that we have specified the mean equation using an explicit expression. Using the explicit expression is for illustration purposes only; we could just as well entered “dlog(ibm) c dlog(spx)” as our specification.
The Power ARCH (PARCH) Model
Taylor (1986) and Schwert (1989) introduced the standard deviation GARCH model, where the standard deviation is modeled rather than the variance. This model, along with several other models, is generalized in Ding
et al. (1993) with the Power ARCH specification. In the Power ARCH model, the power parameter
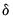
of the standard deviation can be estimated rather than imposed, and the optional
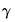
parameters are added to capture asymmetry of up to order
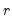
:
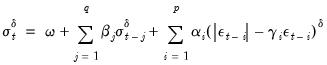 | (27.23) |
where
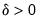
,
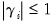
for
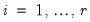
,
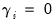
for all
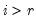
, and
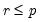
.
The symmetric model sets
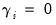
for all
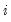
. Note that if
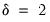
and
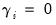
for all
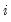
, the PARCH model is simply a standard GARCH specification. As in the previous models, the asymmetric effects are present if
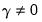
.
To estimate this model, simply select the PARCH in the model specification dropdown menu and input the orders for the , and terms. EViews provides you with the option of either estimating or fixing a value for
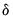
. To estimate the Taylor-Schwert's model, for example, you will to set the order of the asymmetric terms to zero and will set
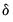
to 1.
The Component GARCH (CGARCH) Model
The conditional variance in the GARCH(1, 1) model:
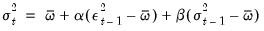 | (27.24) |
shows mean reversion to
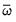
, which is a constant for all time. By contrast, the component model allows mean reversion to a varying level
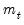
, modeled as:
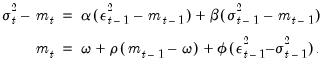 | (27.25) |
Here
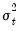
is still the volatility, while
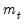
takes the place of
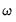
and is the time varying long-run volatility. The first equation describes the transitory component,
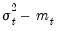
, which converges to zero with powers of (
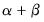
). The second equation describes the long run component
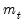
, which converges to
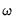
with powers of
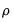
.
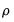
is typically between 0.99 and 1 so that
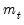
approaches
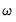
very slowly. We can combine the transitory and permanent equations and write:
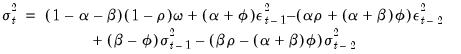 | (27.26) |
which shows that the component model is a (nonlinear) restricted GARCH(2, 2) model.
To select the Component ARCH model, simply choose in the dropdown menu. You can include exogenous variables in the conditional variance equation of component models, either in the permanent or transitory equation (or both). The variables in the transitory equation will have an impact on the short run movements in volatility, while the variables in the permanent equation will affect the long run levels of volatility.
An asymmetric Component ARCH model may be estimated by checking the checkbox. This option combines the component model with the asymmetric TARCH model, introducing asymmetric effects in the transitory equation and estimates models of the form:
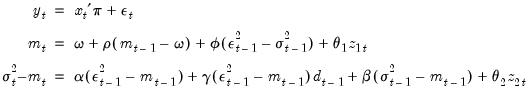 | (27.27) |
where
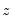
are the exogenous variables and
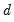
is the dummy variable indicating negative shocks.
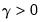
indicates the presence of transitory leverage effects in the conditional variance.
Fractionally Integrated GARCH and EGARCH
EViews 12 estimates Fractionally Integrated GARCH (FIGARCH) models, with support for both standard FIGARCH and Fractionally Integrated Exponential GARCH (FIEGARCH) specifications. The following discussion outlines the basic model and the interactive tools for estimating and working with FIGARCH models.
The Fractionally Integrated GARCH (FIGARCH) Model
While traditional GARCH models focus on short term dynamics of conditional variance, the fractionally integrated GARCH model (FIGARCH) model, introduced by Baillie, Bollerslev and Mikkelsen (1996, BBM), is designed to capture long run dependence properties of the variance.
Background
A standard GARCH model’s specification of the variance may be written as,
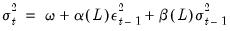 | (27.28) |
where
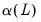
and
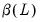
represent polynomial lags,
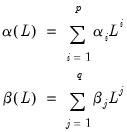 | (27.29) |
and
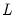
is the lag operator.
The fractionally integrated GARCH (FIGARCH) model modifies this specification by introducing a fractional difference term. The FIGARCH variance may be written as,
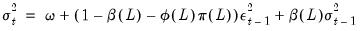 | (27.30) |
where
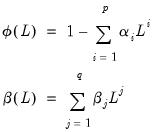 | (27.31) |
and
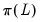
is the infinite lag operator
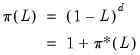 | (27.32) |
which uses the infinite lag expansion
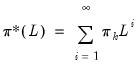 | (27.33) |
In practice, the infinite lag expansion is truncated to a finite number. For example, BBM suggest truncation at 1000 lags.
Estimating a FIGARCH model
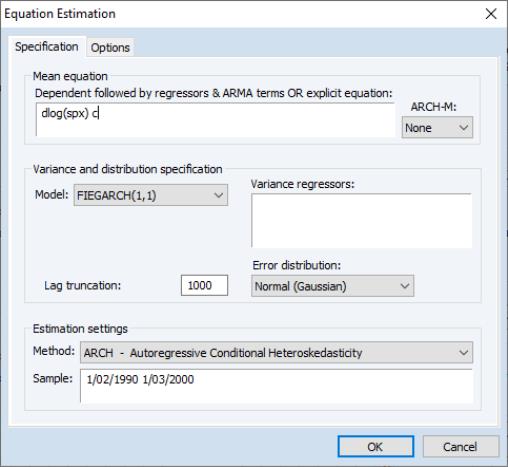
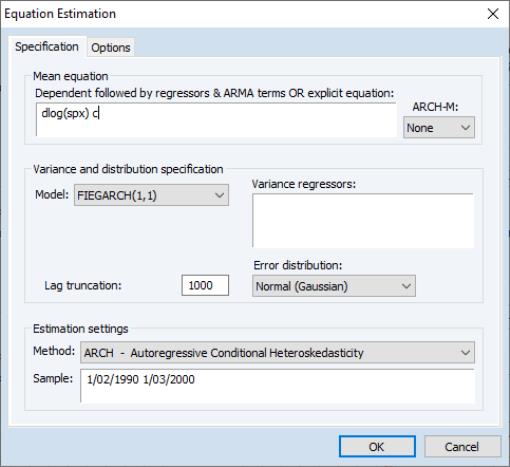
To estimate a FIGARCH model, select in the dropdown at the bottom of the dialog to display the GARCH dialog, then, in the section, choose in the dropdown menu:
As in other GARCH models, in the section of the dialog, you should enter your variables or explicit equation and select your specification.
You may select the and orders, list any , and select the .
Lastly, you may specify the FIGARCH number of terms in the FIGARCH infinite lag specification.
The Fractionally Integrated Exponential GARCH (FIEGARCH) Model
The FIEGARCH model of Bollerslev and Mikkelsen (1996) adds FIGARCH long-memory innovations to EGARCH processes.
Background
Before proceeding, note that while FIEGARCH models can be specified for arbitrary ARCH and GARCH orders, researchers typically restrict both to a single lag, and EViews currently supports only these FIEGARCH(1,1) models.
The starting point for FIEGARCH is an EGARCH model that differs slightly from the model typically estimated by EViews (Equation 26.22). The log conditional variance for this new form of the EGARCH model variance is
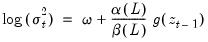 | (27.34) |
where
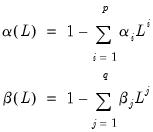 | (27.35) |
and
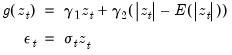 | (27.36) |
For
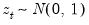
, substituting
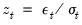
yields the EGARCH(1, 1) variance specification
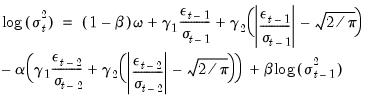 | (27.37) |
which may be compared with the corresponding EGARCH(1, 1) using the EViews (Equation 26.22) alternative specification
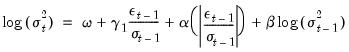 | (27.38) |
The FIEGARCH model adds a long-run lag polynomial to
Equation (27.34)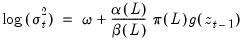 | (27.39) |
The corresponding FIEGARCH(1, 1) is given by
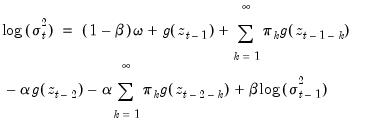 | (27.40) |
Substituting using
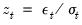
yields
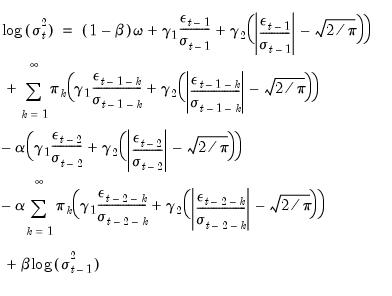 | (27.41) |
As with the FIGARCH model, in practice the infinite sums are truncated at a finite number, typically 1,000 terms.
Estimating a FIEGARCH model
To estimate a FIEGARCH model in EViews simply select in the dropdown at the bottom of the dialog to display the GARCH dialog, then choose FIEGARCH in the section Model dropdown menu.
Note that since as EViews only supports the FIEGARCH(1, 1) specification, you may not specify the number of ARCH and GARCH terms.
You may, as for standard FIGARCH estimation, specify the Lag truncation number.
User Specified Models
In some cases, you might wish to estimate an ARCH model not mentioned above, for example a special variant of PARCH. Many other ARCH models can be estimated using the logl object. For example,
“The Log Likelihood (LogL) Object” contains examples of using logl objects for simple bivariate GARCH models.
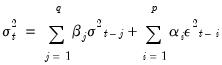
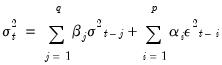
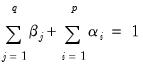
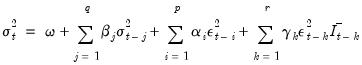
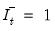 if
if 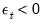 and 0 otherwise.
and 0 otherwise.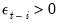 , and bad news.
, and bad news. 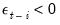 , have differential effects on the conditional variance; good news has an impact of
, have differential effects on the conditional variance; good news has an impact of 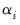 , while bad news has an impact of
, while bad news has an impact of 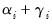 . If
. If 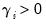 , bad news increases volatility, and we say that there is a leverage effect for the i-th order. If
, bad news increases volatility, and we say that there is a leverage effect for the i-th order. If 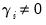 , the news impact is asymmetric.
, the news impact is asymmetric.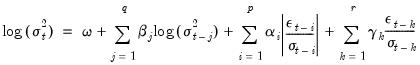
 . The impact is asymmetric if
. The impact is asymmetric if  .
.  follows a Generalized Error Distribution (GED), while EViews offers you a choice of normal, Student’s t-distribution, or GED. Second, Nelson's specification for the log conditional variance is a restricted version of:
follows a Generalized Error Distribution (GED), while EViews offers you a choice of normal, Student’s t-distribution, or GED. Second, Nelson's specification for the log conditional variance is a restricted version of: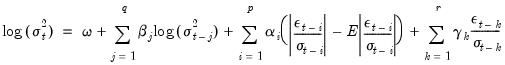
 , which will differ in a manner that depends upon the distributional assumption and the order
, which will differ in a manner that depends upon the distributional assumption and the order  . For example, in a
. For example, in a  model with a normal distribution, the difference will be
model with a normal distribution, the difference will be 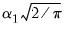 .
. 
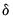 of the standard deviation can be estimated rather than imposed, and the optional
of the standard deviation can be estimated rather than imposed, and the optional 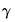 parameters are added to capture asymmetry of up to order
parameters are added to capture asymmetry of up to order 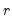 :
: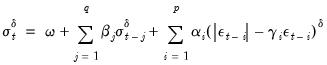
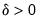 ,
, 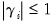 for
for 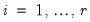 ,
, 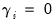 for all
for all 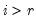 , and
, and 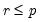 .
.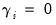 for all
for all 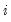 . Note that if
. Note that if 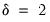 and
and 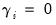 for all
for all 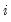 , the PARCH model is simply a standard GARCH specification. As in the previous models, the asymmetric effects are present if
, the PARCH model is simply a standard GARCH specification. As in the previous models, the asymmetric effects are present if 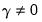 .
.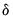 . To estimate the Taylor-Schwert's model, for example, you will to set the order of the asymmetric terms to zero and will set
. To estimate the Taylor-Schwert's model, for example, you will to set the order of the asymmetric terms to zero and will set 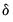 to 1.
to 1.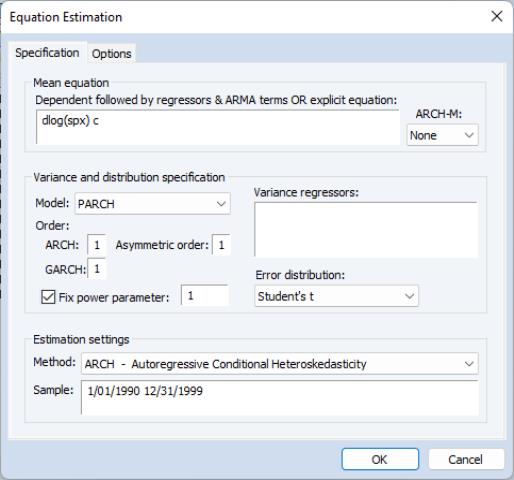
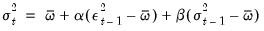
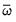 , which is a constant for all time. By contrast, the component model allows mean reversion to a varying level
, which is a constant for all time. By contrast, the component model allows mean reversion to a varying level 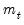 , modeled as:
, modeled as: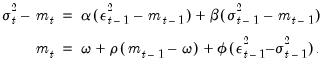
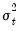 is still the volatility, while
is still the volatility, while 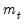 takes the place of
takes the place of 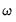 and is the time varying long-run volatility. The first equation describes the transitory component,
and is the time varying long-run volatility. The first equation describes the transitory component, 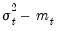 , which converges to zero with powers of (
, which converges to zero with powers of (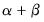 ). The second equation describes the long run component
). The second equation describes the long run component 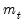 , which converges to
, which converges to 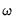 with powers of
with powers of 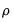 .
. 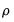 is typically between 0.99 and 1 so that
is typically between 0.99 and 1 so that 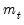 approaches
approaches 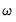 very slowly. We can combine the transitory and permanent equations and write:
very slowly. We can combine the transitory and permanent equations and write: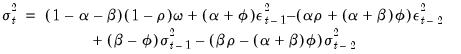
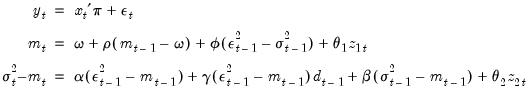
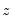 are the exogenous variables and
are the exogenous variables and 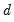 is the dummy variable indicating negative shocks.
is the dummy variable indicating negative shocks. 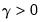 indicates the presence of transitory leverage effects in the conditional variance.
indicates the presence of transitory leverage effects in the conditional variance.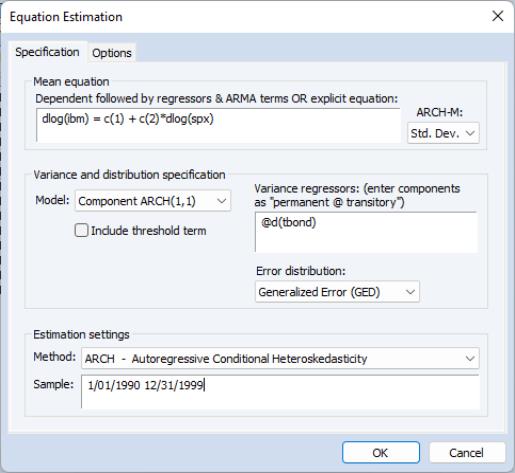
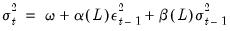
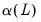 and
and 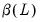 represent polynomial lags,
represent polynomial lags, 
 is the lag operator.
is the lag operator.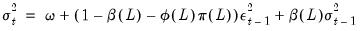
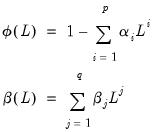
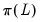 is the infinite lag operator
is the infinite lag operator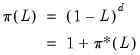
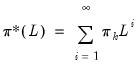
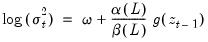
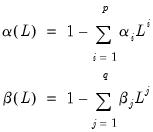
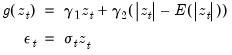
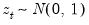 , substituting
, substituting 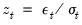 yields the EGARCH(1, 1) variance specification
yields the EGARCH(1, 1) variance specification 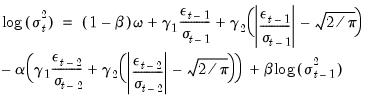
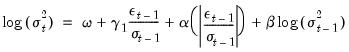
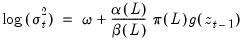
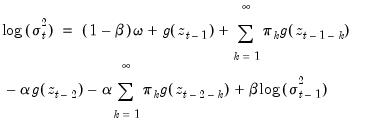
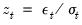 yields
yields