Background
If
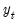
is the dependent (autoregressive) variable,
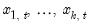
are
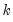
distributed-lag explanatory variables, and
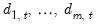
are
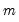
exogenous, potentially deterministic variables, the
Intertemporal Dynamics (ITD) representation of an ARDL(
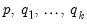
) model is given by:
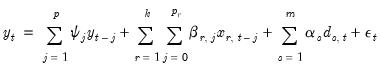 | (29.1) |
where
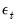
are the innovations, and
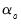
,
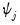
, and
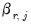
are the coefficients associated with the exogenous variables,
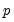
lags of
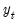
, and
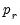
lags of the
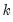
distributed lag regressors
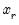
, respectively.
Let
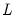
be the usual lag operator and define the lag polynomials:
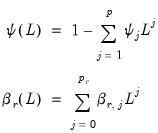 | (29.2) |
Substituting into
Equation (29.1) yields:
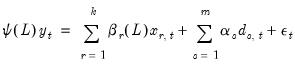 | (29.3) |
Noting that any series
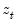
may be written as
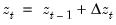
and performing a Beveridge-Nelson decomposition on both
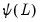
and the
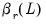
in
Equation (29.3) produces the
Conditional Error Correction (CEC) representation of the ARDL,
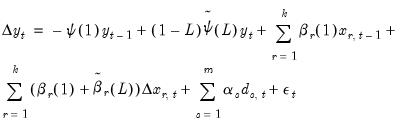 | (29.4) |
which, with a bit of manipulation, may be rewritten as
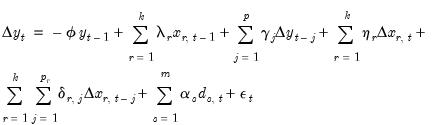 | (29.5) |
where
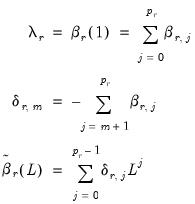 | (29.6) |
and
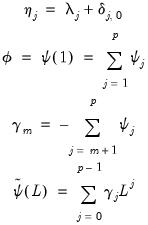 | (29.7) |
Since CEC
Equation (29.5) and
Equation (29.8) are derived from ITD
Equation (29.1), there is an obvious one-to-one correspondence between the two. As with the vector error correction (VEC) form of a VAR, the CEC form offers easy identification of a cointegrating relationship between the dependent variable and the explanatory variables in the ARDL. We discuss this parallel in greater depth in
“Relationship to Vector Error Correction (VEC) Models”.
Rearrange terms, we may re-write
Equation (29.8) as
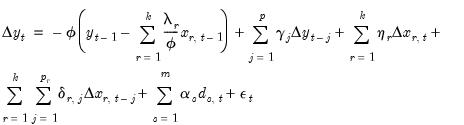 | (29.8) |
If we define the equilibrium error correction term,
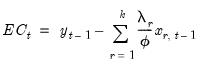 | (29.9) |
then
Equation (29.8) may be written in Error Correction (EC) form:
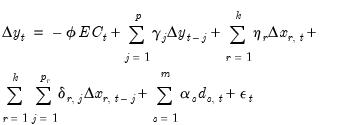 | (29.10) |
where
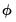
is the error correction parameter, and the long-term equilibrium parameters for the explanatory variables are given by
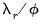
, for
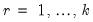
.
Conveniently, the coefficients in both the ITD and the CEC representations of the ARDL model may be estimated via least squares.
Relationship to Vector Error Correction (VEC) Models
Assuming the same lag across the distributed-lag regressors
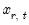
and that the deterministics
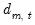
consist of a simple constant and linear trend, Pesaran (2001) demonstrates that the ARDL CEC representation in
Equation (29.8) is in fact the CEC of the VAR(
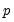
) model:
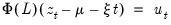 | (29.11) |
where
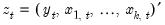
is a
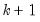
vector of endogenous variables,
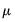
and
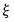
are the
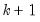
vectors of intercept and trend coefficients, respectively, and
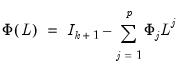 | (29.12) |
is the
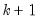
matrix lag polynomial.
Invoking the BN decomposition on
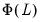
and with following some rearrangement, the CEC representation of this VEC may be written as
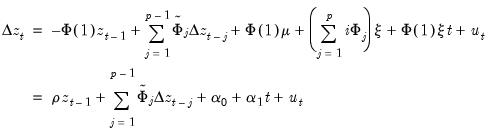 | (29.13) |
where
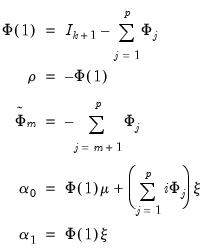 | (29.14) |
which is equivalent to
Equation (29.5).
Nonlinear (asymmetric) ARDL
The classical ARDL framework assumes that the long-run relationship
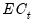
is a symmetric linear combination of regressors. While this is a natural starting assumption, it does not match the behavioral finance and economics literature approach to modeling nonlinearity and asymmetry (Kahneman, Tversky, and Shiller, 1979). In response, Shin (2014) proposes a nonlinear ARDL (NARDL) framework in which short-run and long-run nonlinearities are modeled as positive and negative partial sum decompositions of the explanatory variables.
Consider the partial sum decomposition of a variable
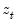
around a threshold of
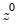
as
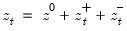
where
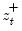
and
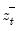
are the partial sum processes of positive and negative
changes in
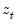
, respectively:
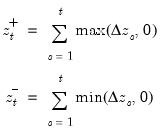 | (29.15) |
The ITD representation of a NARDL(
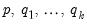
) model is given by:
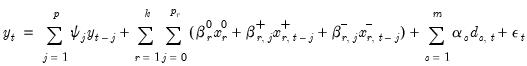 | (29.16) |
where
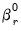
are coefficients for the initial conditions, and where
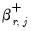
and
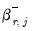
are coefficients associated with the asymmetric distributed-lag variables.
We may an obtain a CEC representation of the ITD NARDL model,
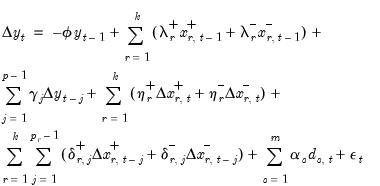 | (29.17) |
where the
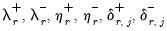
are asymmetric analogues of the coefficients in
Equation (29.6).
We may rearrange terms so that
Equation (29.17) becomes
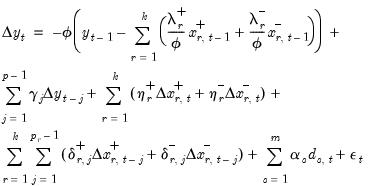 | (29.18) |
Then, define the asymmetric equilibrium error correction term,
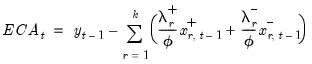 | (29.19) |
so that the CEC
Equation (29.18) may be written in EC form:
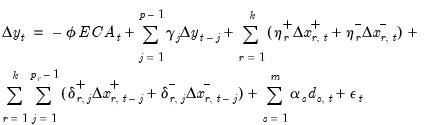 | (29.20) |
where
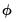
is the error correction parameter, the long-term equilibrium parameters for the explanatory variables are given by
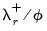
and
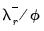
for
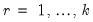
. The short-run parameters for the explanatory variables are given by the
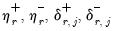
.
Notice that because the CEC representation decomposes the effect of the distribution lag variables into short and long-run components, it allows for asymmetries in various combinations of short and long-run dynamics. This flexibility does not exist in the ITD representation.
As with their symmetric counterparts, NARDL models may be estimated via least squares. This result is appealing since nonlinear models often require iterative estimation routines. Furthermore, bounds testing procedures (
“Bounds Test View”) remain valid and require no meaningful adjustments.
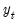 is the dependent (autoregressive) variable,
is the dependent (autoregressive) variable, 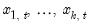 are
are 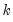 distributed-lag explanatory variables, and
distributed-lag explanatory variables, and 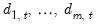 are
are 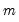 exogenous, potentially deterministic variables, the Intertemporal Dynamics (ITD) representation of an ARDL(
exogenous, potentially deterministic variables, the Intertemporal Dynamics (ITD) representation of an ARDL(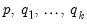 ) model is given by:
) model is given by: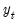 is the dependent (autoregressive) variable,
is the dependent (autoregressive) variable, 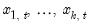 are
are 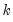 distributed-lag explanatory variables, and
distributed-lag explanatory variables, and 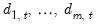 are
are 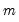 exogenous, potentially deterministic variables, the Intertemporal Dynamics (ITD) representation of an ARDL(
exogenous, potentially deterministic variables, the Intertemporal Dynamics (ITD) representation of an ARDL(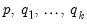 ) model is given by:
) model is given by: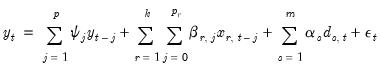
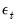 are the innovations, and
are the innovations, and 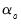 ,
, 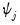 , and
, and 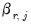 are the coefficients associated with the exogenous variables,
are the coefficients associated with the exogenous variables, 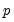 lags of
lags of 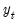 , and
, and 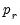 lags of the
lags of the 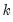 distributed lag regressors
distributed lag regressors 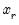 , respectively.
, respectively.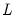 be the usual lag operator and define the lag polynomials:
be the usual lag operator and define the lag polynomials: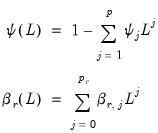
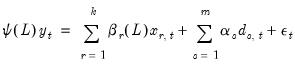
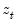 may be written as
may be written as 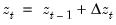 and performing a Beveridge-Nelson decomposition on both
and performing a Beveridge-Nelson decomposition on both 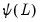 and the
and the 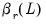 in
in
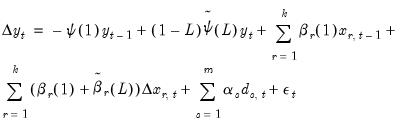
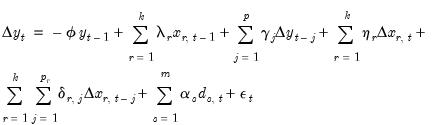
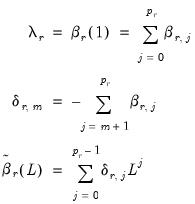
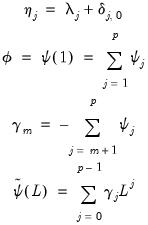
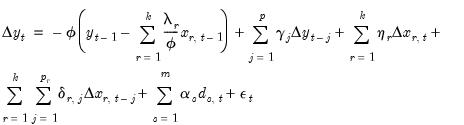
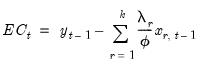
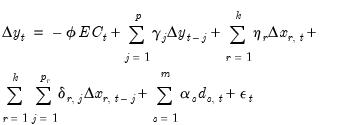
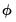 is the error correction parameter, and the long-term equilibrium parameters for the explanatory variables are given by
is the error correction parameter, and the long-term equilibrium parameters for the explanatory variables are given by 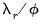 , for
, for 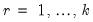 .
. 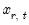 and that the deterministics
and that the deterministics 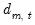 consist of a simple constant and linear trend, Pesaran (2001) demonstrates that the ARDL CEC representation in
consist of a simple constant and linear trend, Pesaran (2001) demonstrates that the ARDL CEC representation in
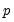 ) model:
) model: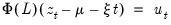
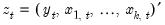 is a
is a 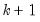 vector of endogenous variables,
vector of endogenous variables, 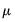 and
and 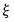 are the
are the 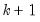 vectors of intercept and trend coefficients, respectively, and
vectors of intercept and trend coefficients, respectively, and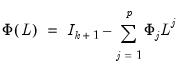
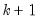 matrix lag polynomial.
matrix lag polynomial.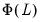 and with following some rearrangement, the CEC representation of this VEC may be written as
and with following some rearrangement, the CEC representation of this VEC may be written as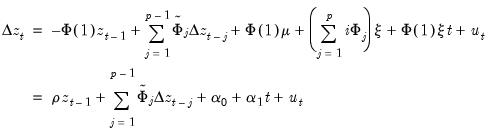
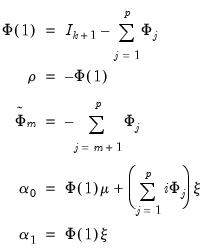
 is a symmetric linear combination of regressors. While this is a natural starting assumption, it does not match the behavioral finance and economics literature approach to modeling nonlinearity and asymmetry (Kahneman, Tversky, and Shiller, 1979). In response, Shin (2014) proposes a nonlinear ARDL (NARDL) framework in which short-run and long-run nonlinearities are modeled as positive and negative partial sum decompositions of the explanatory variables.
is a symmetric linear combination of regressors. While this is a natural starting assumption, it does not match the behavioral finance and economics literature approach to modeling nonlinearity and asymmetry (Kahneman, Tversky, and Shiller, 1979). In response, Shin (2014) proposes a nonlinear ARDL (NARDL) framework in which short-run and long-run nonlinearities are modeled as positive and negative partial sum decompositions of the explanatory variables.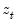 around a threshold of
around a threshold of 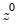 as
as 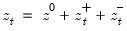 where
where 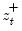 and
and 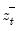 are the partial sum processes of positive and negative
are the partial sum processes of positive and negative 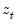 , respectively:
, respectively: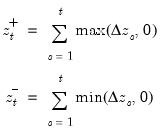
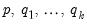 ) model is given by:
) model is given by: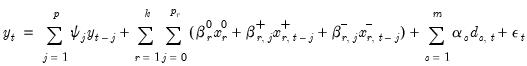
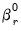 are coefficients for the initial conditions, and where
are coefficients for the initial conditions, and where 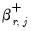 and
and 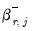 are coefficients associated with the asymmetric distributed-lag variables.
are coefficients associated with the asymmetric distributed-lag variables.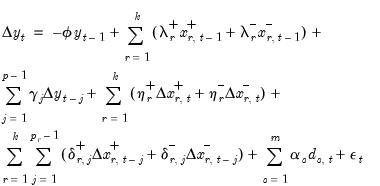
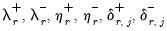 are asymmetric analogues of the coefficients in
are asymmetric analogues of the coefficients in
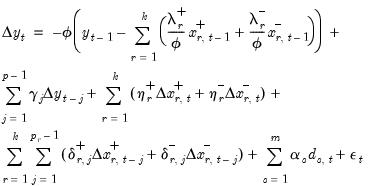
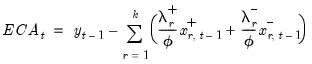
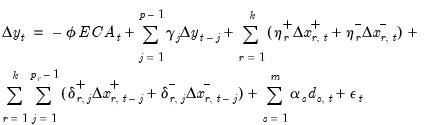
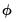 is the error correction parameter, the long-term equilibrium parameters for the explanatory variables are given by
is the error correction parameter, the long-term equilibrium parameters for the explanatory variables are given by 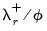 and
and 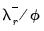 for
for 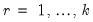 . The short-run parameters for the explanatory variables are given by the
. The short-run parameters for the explanatory variables are given by the 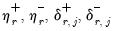 .
.