Estimating ARDL Models in EViews
Since ARDL models are least squares regressions using lags of the dependent and independent variables as regressors, they can be estimated in EViews using an equation object with the Least Squares estimation method.
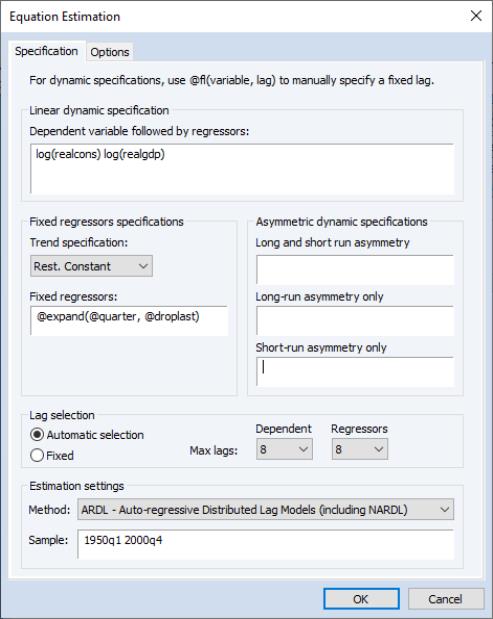
However, EViews also offers a specialized estimator for handling ARDL models. This estimator offers built-in lag-length selection methods, as well as post-estimation views. To estimate an ARDL model using the ARDL estimator, open the equation dialog by selecting , or by selecting and then selecting ARDL from the Method dropdown menu. EViews will then display the ARDL estimation dialog:
The Specification tab allows you to specify the variables used in the regression, and whether to let EViews automatically detect the appropriate number of lags for each variable.
To begin, enter the name of the dependent variable, followed by a space delimited list of dynamic regressors (
i.e., variables which will have lag terms in the model) in the
Dynamic Specification edit box. You may then select whether you wish EViews to automatically select the number of lags for all variables by selecting the Automatic Selection radio button, fixing the independent variable and the regressors to a uniform fixed length by selecting the Fixed radio buttons, or by taking full control of granularity and specifying a specific lag for each of the independent and regressors variables. The latter can be specified via command in the Dynamic Specification edit box by replacing each variable by the Fixed Lag command @FL(VARIABLE, LAG). For instance, if the variable
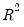
should possess 3 lags, then one would specify this by writing @FL(
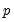
, 3). One can do this for all variables in order to estimate a specific structure, or specify some variables using the @FL command, and others without. In the latter case, if the Automatic Selection radio button is selected, EViews will fix the lags of the variables specified with @FL, and automatically select the lags for the variables which were not specified using the @FL function. Alternatively, if the Fixed radio button is selected, any variables not specified with @FL will have the specified fixed number.
If you choose automatic selection, you must then select the maximum number of lags to test for the dependent variable and regressors using the Max lags dropdowns. If you select to use a fixed number of lags, the same dropdowns can be used to select the number of lags for the dependent variable and regressors. Note that when using fixed lags for regressors, each regressor will be given the same number of lags.
The Fixed regressors area lets you specify any fixed/static variables (regressors without lags). The Trend specification dropdown may be used to specify which of the five cases for the trend and intercept should be included. Any other static regressors can be specified by entering their name in the List of fixed regressors box.
The Options tab allows you to specify the type of model selection to be used if you chose automatic selection on the Specification tab. You may choose between the Akaike Information Criterion (AIC), Schwarz Criterion (SC), Hannan-Quinn Criterion (HQ), or the Adjusted R-squared.
You may also select the type of covariance matrix to use in the final estimates, using the Coefficient covariance matrix dropdown. Note that this selection does not affect the model selection criteria.
ARDL Post-Estimation Views and Procedures
Since ARDL models are estimated by simple least squares, all of the views and procedures available to equation objects estimated by least squares are also available for ARDL models. In addition, there are a few ARDL specific views.
The item on the menu allows you to view either a or a . The graph shows the model selection value for the twenty “best” models. If you use either the Akaike Information Criterion (AIC), the Schwarz Criterion (BIC), or the Hannan-Quinn (HQ) criterion, the graph will show the twenty models with the lowest criterion value. If you choose the Adjusted R-squared as the model selection criteria, the graph will show the twenty models with the highest Adjusted R-squared. The table form of the view shows the log-likelihood value, the AIC, BIC and HQ values, and the Adjusted R-squareds of the top twenty models in tabular form.
The menu offers the new item Every ARDL model is associated with a CEC model. This view displays a table of least squares estimates corresponding to this CEC regression. Note that the lag of the dependent variable in this regression will always be suffixed by a single asterisk while some other variables will be suffixed by a double asterisk. As summarized in notes below the regression output, the single asterisk indicates that the p-value associated with the relevant variable is incompatible with the t-Bounds distribution in Theorem 3.2 in PSS(2001). Moreover, any variables suffixed by a double asterisk indicates a dynamic regressor with an optimal lag of zero. As such, EViews does not include lags and differences of such variables, but estimates them contemporaneously. Accordingly, such variables should be reinterpreted in the context of the decomposition
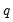
so that they can be included in the
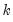
term which arises in each of the CEC regressions. In particular, least squares estimates of coefficients associated with such variables are simultaneously estimates of the coefficients associated with
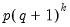
as well as
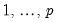
. When this is the case, EViews augments the table of regression estimates with a note that such variables should be interpreted as Z = Z(-1) + D(Z).
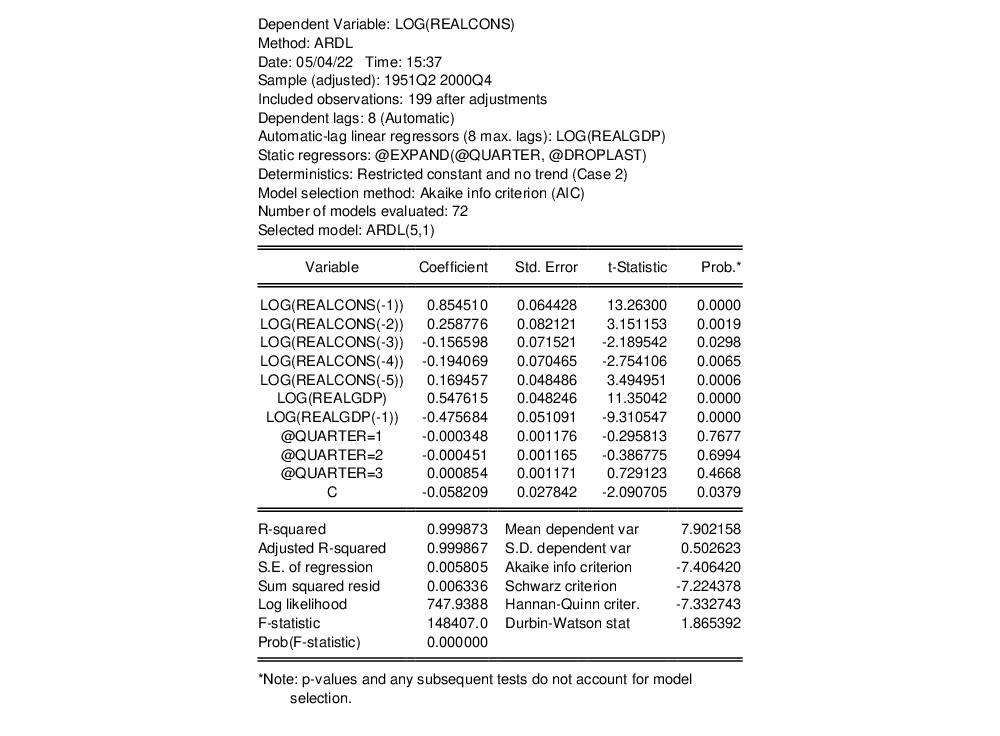
There are also several tables provided in this view. The first table is titled
Levels Equation and displays the estimates of long-run variables, their standard errors computed using the delta method as in PS(98), their
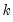
-statistics, as well as the appropriate
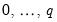
-values. Moreover, just below this table is a line starting with
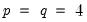
. This expression lists the name of the dependent variable minus an expression enclosed in brackets. This is the long run, otherwise known as the error correction equation.
Below the table of long run coefficient estimates are two additional tables, respectively titled as the
-Bounds Test and the
-Bounds Test. These tables respectively display the the the
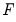
- and
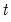
- statistics along with their associated I(0) (lower) and I(1) (upper) critical value bounds for the null hypotheses of no levels relationship between the dependent variable and the regressors in the CEC model. The critical values are provided for significance levels 10%, 5%, 2.5%, and 1%, respectively. The
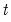
-Bounds test in particular is a parameter significance test on the lagged value of the dependent variable. Since the distribution of this test is non-standard, the
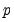
-value provided in the regression output of the CEC regression is not compatible with this distribution, although the
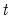
-statistic is valid. Accordingly, any inference must be conducted using the
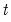
-Bounds test critical values provided.
We also mention here that the
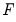
- critical value tables now present the critical values computed under an asymptotic regime (sample size equal to 1000) and referenced from PSS(2001), in addition to providing cirtical values for finite sample regimes (sample sizes running from 30 to 80 in increments of 5) and referenced from Narayan (2005).
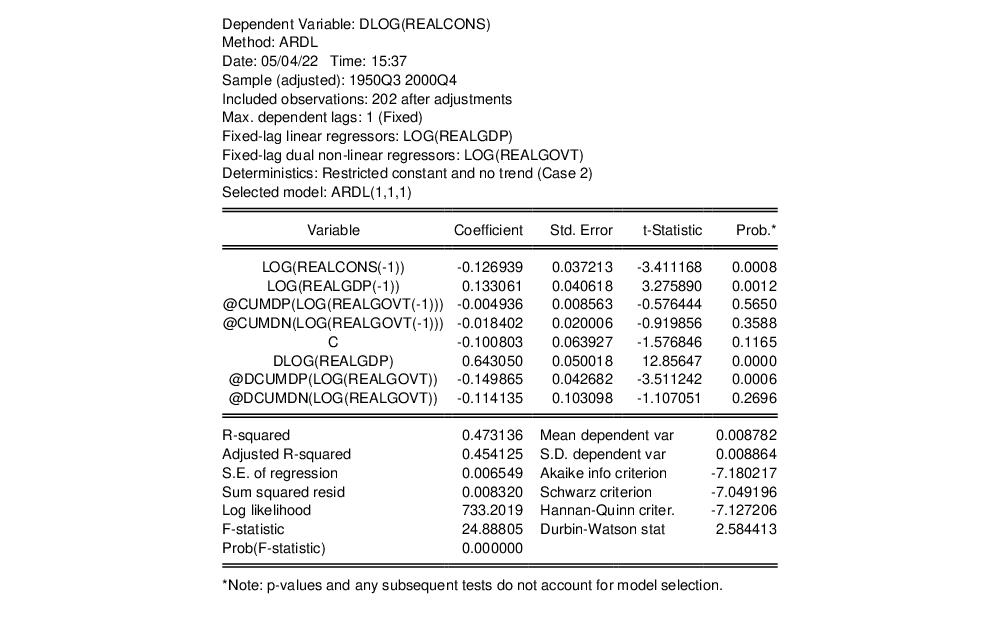
Another view that is offered after estimation is . In this view, an error correction model which estimates the speed of adjustment to equilibrium in a cointegrating relationship. Here, the error correction term derived as the Levels Equation earlier, is included among the regressors and is denoted as
CointEq. The coefficient associated with this regressor is typically the speed of adjustment to equilibrium in every period. If variables are indeed cointegrated, we typically expect this coefficient to be negative and highly significant. Here as well we find the the
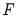
-Bounds Test and the
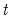
-Bounds Test tables below the regression output. While the the
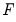
-Bounds Test will not have changed from the view, the
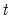
-Bounds Test here reflects the
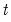
- statistic associated with the
CointEq regressor. Again, since the distribution of this test is non-standard, the
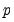
-value provided in the regression output is not compatible with this distribution and any inference must be conducted using the the
-Bounds test critical values provided.
Issues with ARDL Model Selection
The ARDL model selection process will use the same sample for each estimation. Since the selection is over the number of lags, this means that observations will be dropped from each estimation based on the maximum number of lags in the selection procedure. However the final estimation output will use all observations available for the selected model. Consequently, unless the selected model happens to be the model with the maximum number of lags, the final estimation will have more observations than when that model was estimated during selection, and will have different estimated results.

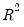 should possess 3 lags, then one would specify this by writing @FL(
should possess 3 lags, then one would specify this by writing @FL(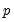 , 3). One can do this for all variables in order to estimate a specific structure, or specify some variables using the @FL command, and others without. In the latter case, if the Automatic Selection radio button is selected, EViews will fix the lags of the variables specified with @FL, and automatically select the lags for the variables which were not specified using the @FL function. Alternatively, if the Fixed radio button is selected, any variables not specified with @FL will have the specified fixed number.
, 3). One can do this for all variables in order to estimate a specific structure, or specify some variables using the @FL command, and others without. In the latter case, if the Automatic Selection radio button is selected, EViews will fix the lags of the variables specified with @FL, and automatically select the lags for the variables which were not specified using the @FL function. Alternatively, if the Fixed radio button is selected, any variables not specified with @FL will have the specified fixed number.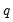 so that they can be included in the
so that they can be included in the 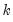 term which arises in each of the CEC regressions. In particular, least squares estimates of coefficients associated with such variables are simultaneously estimates of the coefficients associated with
term which arises in each of the CEC regressions. In particular, least squares estimates of coefficients associated with such variables are simultaneously estimates of the coefficients associated with 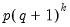 as well as
as well as 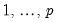 . When this is the case, EViews augments the table of regression estimates with a note that such variables should be interpreted as Z = Z(-1) + D(Z).
. When this is the case, EViews augments the table of regression estimates with a note that such variables should be interpreted as Z = Z(-1) + D(Z). 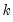 -statistics, as well as the appropriate
-statistics, as well as the appropriate 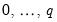 -values. Moreover, just below this table is a line starting with
-values. Moreover, just below this table is a line starting with 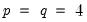 . This expression lists the name of the dependent variable minus an expression enclosed in brackets. This is the long run, otherwise known as the error correction equation.
. This expression lists the name of the dependent variable minus an expression enclosed in brackets. This is the long run, otherwise known as the error correction equation. -Bounds Test and the
-Bounds Test and the  -Bounds Test. These tables respectively display the the the
-Bounds Test. These tables respectively display the the the 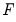 - and
- and 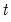 - statistics along with their associated I(0) (lower) and I(1) (upper) critical value bounds for the null hypotheses of no levels relationship between the dependent variable and the regressors in the CEC model. The critical values are provided for significance levels 10%, 5%, 2.5%, and 1%, respectively. The
- statistics along with their associated I(0) (lower) and I(1) (upper) critical value bounds for the null hypotheses of no levels relationship between the dependent variable and the regressors in the CEC model. The critical values are provided for significance levels 10%, 5%, 2.5%, and 1%, respectively. The 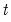 -Bounds test in particular is a parameter significance test on the lagged value of the dependent variable. Since the distribution of this test is non-standard, the
-Bounds test in particular is a parameter significance test on the lagged value of the dependent variable. Since the distribution of this test is non-standard, the 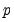 -value provided in the regression output of the CEC regression is not compatible with this distribution, although the
-value provided in the regression output of the CEC regression is not compatible with this distribution, although the 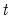 -statistic is valid. Accordingly, any inference must be conducted using the
-statistic is valid. Accordingly, any inference must be conducted using the 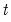 -Bounds test critical values provided.
-Bounds test critical values provided.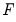 - critical value tables now present the critical values computed under an asymptotic regime (sample size equal to 1000) and referenced from PSS(2001), in addition to providing cirtical values for finite sample regimes (sample sizes running from 30 to 80 in increments of 5) and referenced from Narayan (2005).
- critical value tables now present the critical values computed under an asymptotic regime (sample size equal to 1000) and referenced from PSS(2001), in addition to providing cirtical values for finite sample regimes (sample sizes running from 30 to 80 in increments of 5) and referenced from Narayan (2005).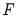 -Bounds Test and the
-Bounds Test and the 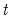 -Bounds Test tables below the regression output. While the the
-Bounds Test tables below the regression output. While the the 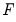 -Bounds Test will not have changed from the Long Run Form and Bounds Test view, the
-Bounds Test will not have changed from the Long Run Form and Bounds Test view, the 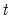 -Bounds Test here reflects the
-Bounds Test here reflects the 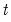 - statistic associated with the CointEq regressor. Again, since the distribution of this test is non-standard, the
- statistic associated with the CointEq regressor. Again, since the distribution of this test is non-standard, the 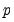 -value provided in the regression output is not compatible with this distribution and any inference must be conducted using the the
-value provided in the regression output is not compatible with this distribution and any inference must be conducted using the the 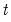 -Bounds test critical values provided.
-Bounds test critical values provided.