Perform an orthogonal or oblique factor rotation of the loadings of an estimated factor object.
Syntax
factor_name.rotate(options)
You may use the “type=” and “method=” options to select from a variety of rotations methods.
Method Options
The first five options control the basic rotation specification:
type=arg (default=“orthog”) | Orthogonal (“orthog”) or oblique (“oblique”) rotation (ignored if method is not supported, e.g, “orthogonal Harris-Kaiser” or “oblique Entropy Ratio”). |
method=arg (default=“varimax”) | Method (objective) for the rotation. See keywords below |
param=arg | Rotation parameter, if applicable (see description below). |
preparam=arg (default=1, Varimax) | Orthomax pre-rotation parameter (for “method=hk” and “method=promax”). |
The following rotation methods are supported:
| | | |
Biquartimax | biquartimax | • | • |
Crawford-Ferguson | cf | • | • |
Entropy | entropy | • | |
Entropy Ratio | entratio | • | |
Equamax | equamax | • | • |
Factor Parsimony | parsimony | • | • |
Generalized Crawford-Ferguson | gcf | • | • |
Geomin | geomin | • | • |
Harris-Kaiser (case II) | hk | | • |
Infomax | infomax | • | • |
Oblimax | oblimax | | • |
Oblimin | oblimin | | • |
Orthomax | orthomax | • | • |
Parsimax | parsimax | • | • |
Pattern Simplicity | pattern | • | • |
Promax | promax | | • |
Quartimax/Quartimin | quartimax | • | • |
Simplimax | simplimax | • | • |
Tandem I | tandemi | • | |
Tandem II | tandemii | • | |
Target | target | • | • |
Varimax | varimax | • | • |
In selecting a rotation method you should bear in mind the following:
• EViews employs the Crawford-Ferguson variants of the Biquartimax, Equamax, Factor Parsimony, Orthomax, Parsimax, Quartimax, and Varimax objective functions. These objective functions yield the same results as the standard versions in the orthogonal case, but are better behaved (e.g., do not permit factor collapse) under direct oblique rotation (see Browne 2001, p. 118-119). Note that oblique Crawford-Ferguson Quartimax is equivalent to Quartimin.
• The EViews Orthomax objective for parameter
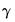
is evaluated using the Crawford-Ferguson objective with factor complexity weight
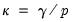
(see
“Types of Rotation”).
Some special cases of Orthomax are Quartimax (
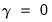
), Varimax (
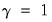
), Equamax (
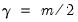
), Parsimax (
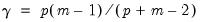
) and Factor Parsimony (
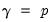
).
• The two orthoblique methods, Promax and Harris-Kaiser both perform an initial orthogonal rotation, followed by a oblique adjustment. For both of these methods, EViews provides some flexibility in the choice of initial rotation. By default, EViews will perform an initial orthogonal Orthomax rotation with the default parameter set to 1 (Varimax). To perform initial rotation with Quartimax, you should set the Orthomax parameter to 0.
Some of the rotation criteria have user-specified parameters that may be specified using the “param=” and (for Harris-Kaiser and Promax) the “preparam=” options. The parameters and their default values are given by:
| | |
Crawford-Ferguson | 1 | Factor complexity weight. The variable complexity weight is 1 minus the factor complexity weight. (default=0, Quartimax) |
Generalized Crawford-Ferguson | 4 | Vector of weights for (in order): total squares, variable complexity, factor complexity, diagonal quartics. (no default) |
Geomin | 1 | Epsilon offset. (default=0.01) |
Harris-Kaiser (case II) | 2 | Power parameter (default=0, independent cluster solution), Orthomax pre-rotation parameter. (default=1, Varimax) |
Oblimin | 1 | Deviation from orthogonality. (default=0, Quartimin) |
Orthomax | 1 | Factor complexity weight. (default=1, Varimax) |
Promax | 2 | Power parameter (default=3), Orthomax pre-rotation parameter (default=1, Varimax). |
Simplimax | 1 | Fraction of near-zero loadings. (default=0.75) |
Target | 1 | Name of 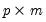 matrix of target loadings. Missing values correspond to unrestricted elements. (no default) |
where
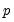
is the number of variables and
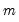
is the number of factors. The remaining options modify the properties of the specified rotation method:
Options
wgts=arg (default=“none”) | Row weighting for loadings: none (“none”), kaiser (“kaiser”), Cureton-Mulaik (“cureton”). |
prior=arg (default =“unrotated”) | Initial rotation matrix: unrotated (“unrotated”), randomly generated (“random”), previous rotation (“previous”), user-specified (“user”). |
ptype=arg (default=“orthog”) | Type of prior random rotation: orthogonal (“orthog”) or oblique (“oblique”). Only relevant if “prior=random” and the main rotation method is oblique. If the main rotation method is orthogonal, random prior rotations will be orthogonalized. |
preps=integer (default=25) | Number of random prior rotations to evaluate (maximum 10000). |
pname=arg | Name of matrix containing prior rotation. |
pseed=positive integer | Seed the random number generator for the prior random rotations. If not specified, EViews will seed the random number generator with a single integer draw from the default global random number generator. |
prnd= arg (default=“kn” or method previously set using
rndseed) | Type of random number generator for the random prior rotation: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”) L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
m=integer | Maximum number of iterations. |
c=scalar | Set convergence criterion. The criterion is based upon the norm of the gradients scaled by the objective function. The criterion will be set to the nearest value between 1e-24 and 0.2. |
showopts / ‑showopts | [Do / do not] display the starting coefficient values and estimation options in the rotation output. |
p | Print rotation results. |
Examples
f1.rotate(type=orthog, method=equamax)
performs an orthogonal rotation with the equamax objective function.
f1.rotate(type=oblique, method=hk, param=.4)
performs a Harris-Kaiser oblique rotation with parameter 0.4
f1.rotate(type=oblique, method=promax, param=.7)
performs a Promax rotation with parameter 0.7
Cross-references
See
“Rotating Factors” for a discussion of factor rotation.
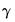 is evaluated using the Crawford-Ferguson objective with factor complexity weight
is evaluated using the Crawford-Ferguson objective with factor complexity weight 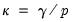 (see
“Types of Rotation”).
(see
“Types of Rotation”). 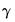 is evaluated using the Crawford-Ferguson objective with factor complexity weight
is evaluated using the Crawford-Ferguson objective with factor complexity weight 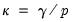 (see
“Types of Rotation”).
(see
“Types of Rotation”). 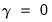 ), Varimax (
), Varimax (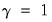 ), Equamax (
), Equamax (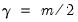 ), Parsimax (
), Parsimax (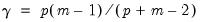 ) and Factor Parsimony (
) and Factor Parsimony (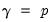 ).
).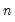
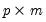 matrix of target loadings. Missing values correspond to unrestricted elements.
matrix of target loadings. Missing values correspond to unrestricted elements.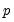 is the number of variables and
is the number of variables and 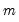 is the number of factors. The remaining options modify the properties of the specified rotation method:
is the number of factors. The remaining options modify the properties of the specified rotation method: