Numeric Expressions
One of the most powerful features of EViews is the ability to use and to process mathematical expressions. EViews contains an extensive library of built-in operators and functions that allow you to perform complicated mathematical operations on your data with just a few keystrokes. In addition to supporting standard mathematical and statistical operations, EViews provides a number of specialized functions for automatically handling the leads, lags and differences that are commonly found in time series data.
An EViews expression is a combination of numbers, series names, functions, and mathematical and relational operators. In practical terms, you will use expressions to describe all mathematical operations involving EViews objects.
As in other programs, you can use these expressions to calculate a new series from existing series, to describe a sample of observations, or to describe an equation for estimation or forecasting. However, EViews goes far beyond this simple use of expressions by allowing you to use expressions virtually anywhere you would use a series. We will have more on this important feature shortly, but first, we describe the basics of using expressions.
Operators
EViews expressions may include operators for the usual arithmetic operations. The operators for addition (+), subtraction (-), multiplication (*), division (/) and raising to a power (^) are used in standard fashion so that:
5 + 6 * 7.0 / 3
7 + 3e-2 / 10.2345 + 6 * 10^2 + 3e3
3^2 - 9
are all valid expressions. Notice that explicit numerical values may be written in integer, decimal, or scientific notation.
In the examples above, the first expression takes 5 and adds to it the product of 6 and 7.0 divided by 3 (5+14=19); the last expression takes 3 raised to the power 2 and subtracts 9 (9 – 9 = 0). These expressions use the order of evaluation outlined below.
The “-” and “+” operators are also used as the unary minus (negation) and unary plus operators. It follows that:
2-2
-2+2
2+++++++++++++-2
2---2
all yield a value of 0.
EViews follows the usual order in evaluating expressions from left to right, with operator precedence order as follows (from highest precedence to lowest):
• unary minus (-), unary plus (+)
• exponentiation (^)
• multiplication (*), division (/)
• addition (+), subtraction (-)
• comparison (<, >, <=, >=, =)
• and, or
The last two sets of operators are used in logical expressions.
To enforce a particular order of evaluation, you can use parentheses. As in standard mathematical analysis, terms which are enclosed in parentheses are treated as a subexpression and evaluated first, from the innermost to the outermost set of parentheses. We strongly recommend the use of parentheses when there is any possibility of ambiguity in your expression.
To take some simple examples,
• -1^2, evaluates to (–1)^2=1 since the unary minus is evaluated prior to the power operator.
• -1 + -2 * 3 + 4, evaluates to –1 + –6 + 4 = –3. The unary minus is evaluated first, followed by the multiplication, and finally the addition.
• (-1 + -2) * (3 + 4), evaluates to –3 * 7 = –21. The unary minuses are evaluated first, followed by the two additions, and then the multiplication.
• 3*((2+3)*(7+4) + 3), evaluates to 3 * (5*11 + 3) = 3 * 58 =174.
A full listing of operators is presented in
“Operators” .
Series Expressions
Much of the power of EViews comes from the fact that expressions involving series operate on every observation, or element, of the series in the current sample. For example, the series expression:
2*y + 3
tells EViews to multiply every sample value of Y by 2 and then to add 3. We can also perform operations that work with multiple series. For example:
x/y + z
indicates that we wish to take every observation for X and divide it by the corresponding observation on Y, and add the corresponding observation for Z.
Series Functions
EViews contains an extensive library of built-in functions that operate on all of the elements of a series in the current sample. Some of the functions are “element functions” which return a value for each element of the series, while others are “summary functions” which return scalars, vectors or matrices, which may then be used in constructing new series or working in the matrix language (see
“Matrix Language” for a discussion of scalar, vector and matrix operations).
Most function names in EViews are preceded by the @-sign. For example, @mean returns the average value of a series taken over the current sample, and @abs takes the absolute value of each observation in the current sample.
All element functions return NAs when any input value is missing or invalid, or if the result is undefined. Functions which return summary information generally exclude observations for which data in the current sample are missing. For example, the @mean function will compute the mean for those observations in the sample that are non-missing.
There is an extensive set of functions that you may use with series:
• Workfile functions that provide information about observations identifiers or allow you to construct time trends are described in
“Workfile Functions”.
The remainder of this chapter will provide additional information on some of these functions, then examples of expressions involving functions.
Series Elements
At times, you may wish to access a particular observation for a series. EViews provides you with a special function, @elem, which allows you to use a specific value of a series.
@elem takes two arguments: the first argument is the name of the series, and the second is a quoted date or observation identifier.
For example, suppose that you want to use the 1980Q3 value of the quarterly series Y, or observation 323 of the undated series X. Then the functions:
@elem(y, "1980Q3")
@elem(x, "323")
will return the values of the respective series in the respective periods.
Numeric Relational Operators
Relational comparisons may be used as part of a mathematical operation, as part of a sample statement, or as part of an if-condition in programs.
A numeric relational comparison is an expression which contains the “=” (equal), “>=” (greater than or equal), “<=” (less than or equal), “<>” (not equal), “>” (greater than), or “<” (less than) comparison operators. These expressions generally evaluate to TRUE or FALSE, returning a 1 or a 0, depending on the result of the comparison.
Comparisons involving strings are discussed in
“String Relational Operators” .
Note that EViews also allows relational comparisons to take the value “missing” or NA, but for the moment, we will gloss over this point until our discussion of missing values (see
“Missing Values”).
We have already seen examples of expressions using relational operators in our discussion of samples and sample objects. For example, we saw the sample condition:
incm > 5000
which allowed us to select observations meeting the specified condition. This is an example of a relational expression—it is TRUE for each observation on INCM that exceeds 5000; otherwise, it is FALSE.
As described above in the discussion of samples, you may use the “and” and “or” conjunction operators to build more complicated expressions involving relational comparisons:
(incm>5000 and educ>=13) or (incm>10000)
It is worth emphasizing the fact that EViews uses the number 1 to represent TRUE and 0 to represent FALSE. This internal representation means that you can create complicated expressions involving logical subexpressions. For example, you can use relational operators to recode your data:
0*(inc<100) + (inc>=100 and inc<200) + 2*(inc>=200)
which yields 0 if INC<100, 1 if INC is greater than or equal to 100 and less than 200, and 2 for INC greater than or equal to 200.
The equality comparison operator “
=” requires a bit more discussion, since the equal sign is used both in assigning values and in comparing values. We consider this issue in greater depth when we discuss creating and modifying series (see
“Series”). For now, note that if used in an expression:
incm = 2000
evaluates to TRUE if INCOME is exactly 2000, and FALSE, otherwise.
Descriptive Statistics
Standard descriptive statistic functions are available in EViews. These include, but are not limited to functions to calculate the mean (
@mean), the median (
@median), the standard deviation (
@stdev), the variance (
@var) and covariance (
@cov). The descriptive statistic functions all take an optional sample as an argument. For a full list of descriptive statistics functions, see
“Basic Statistics” .
It should be noted that EViews offers two ways to calculate standard deviations, variances and covariances. The simple standard deviation function,
@stdev, calculates the sample standard deviation, that is the square root of the sum-of-squares divided by
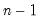
. To calculate the population standard deviation, that is division by
n, use the
@stdevp function. Note for symmetry purposes there is also a
@stdevs which performs the same calculation as
@stdev.
The @var and @cov functions calculate the population variance and covariance respectively, i.e., they divide through by n. To calculate the sample variance or covariance use the @vars or @covs functions. Again, there are also @varp and @covp functions which do the same as @var or @cov.
Leads, Lags, Differences and Time Series Functions
It is easy to work with lags or leads of your series. Simply use the series name, followed by the lag or lead enclosed in parentheses. Lags are specified as negative numbers and leads as positive numbers so that,
income(-4)
is the fourth lag of the income series, while:
sales(2)
is the second lead of sales.
While EViews expects lead and lag arguments to be integers, there is nothing to stop you from putting non-integer values in the parentheses. EViews will automatically convert the number to an integer; you should be warned, however, that the conversion behavior is not guaranteed to be systematic. If you must use non-integer values, you are strongly encouraged to use the @round, @floor, or @ceil functions to control the lag or lead behavior.
In many places in EViews, you can specify a range of lead or lag terms. For example, when estimating equations, you can include expressions of the form:
income(-1 to -4)
to represent all of the INCOME lags from 1 to 4. Similarly, the expressions:
sales sales(-1) sales(-2) sales(-3) sales(-4)
sales(0 to -4)
sales(to -4)
are equivalent methods of specifying the level of SALES and all lags from 1 to 4.
The @lag function can also be used to specify lags. Thus the expressions:
@lag(sales,1)
sales(-1)
are equivalent. Note one useful function of @lag is that it will take the lag of everything within parenthesis. @lag can therefore be used to find the lag of an expression. Typing:
@lag((sales-income)/sales,4)
(sales(-4)-income(-4))/sales(-4)
yields identical results.
EViews also has several built-in functions for working with difference data in either levels or in logs. The “D” and “DLOG” functions will automatically evaluate the differences for you. For example, instead of taking differences explicitly,
income - income(-1)
log(income) - log(income(-1))
you may use the equivalent expressions,
d(income)
dlog(income)
You can take higher order differences by specifying the difference order. For example, the expressions:
d(income,4)
dlog(income,4)
represent the fourth-order differences of INCOME and log(INCOME).
If you wish to take seasonal differences, you should specify both the ordinary, and a seasonal difference term:
d(income,1,4)
dlog(income,1,4)
These commands produce first order differences with a seasonal difference at lag 4. If you want only the seasonal difference, specify the ordinary difference term to be 0:
d(income,0,4)
dlog(income,0,4)
Other time series functions provided by EViews include a number of percentage change type functions. The simplest of these, @pc calculates a simple one-period percentage change in a series. For example typing:
@pca(income)
calculates the annual percentage change in INCOME.
Two special types of time series functions, moving functions and cumulative functions are also available in EViews, and are described below.
A listing of the lags, leads, differences and percentage change functions is provided in
“Series Utility” .
Cumulative and Moving Statistic Functions
Cumulative and moving statistic functions provide information over a range, or “window” of observations. The cumulative functions come in two types, those that move forwards and those that move backwards. The forwards functions, which take the form @cum[stat], have a window that starts at the start of the workfile (or if a sample is given in the function, from the start of the sample) up until the current observation.
The backwards functions, which take the form @cumb[stat], start at the end of the workfile, or sample, and move backwards until the current observation.
Note for both type of cumulative function the length of the window is different for each observation. The cumulative functions may be thought of as perform “running total” type calculations. Missing values are not propagated in the cumulative functions, i.e., observations with a value equal to NA are simply skipped.
The moving statistic functions have a shorter, user specified, window length. They provide information on the n observations up to, and including, the current observation, where n is chosen by the user.
The moving functions come in two types, those that propagate missing values and those that do not. For the functions that do propagate missing values, which take the form @mov[stat], if any of the observations within the window contain an NA the function will return NA. The functions that do not propagate, which take the form @m[stat], will simply skip any NA observations.
For more information on missing values see
“Missing Values”.
As an example, you could find out the maximum value of INCOME from the start of the workfile to each observation by typing:
show @cummax(income)
If the first, say, four observations of INCOME are 100, 120, 110, 140 then this command will show a series as 100, 120, 120, and 140 as the first four observations.
If you wanted to know at each observation the average of the previous 3 years (including the current year) SALES figures you could type:
show @movav(sales,3)
Note this is equal to:
show (sales + sales(-1) + sales(-2))/3
Note that the lag or lead operators can be used inside a moving statistic function to allow you to control the exact start and end point of your window. For example, if you wanted to know, at each observation, the sum of SALES from three years ago, two years ago and last year (i.e. the sum of SALES(-1), SALES(-2) and SALES(-3)) you could type:
show @movsum(sales(-1),3)
Further details and a complete list of cumulative functions can be found in
“Cumulative Statistics”, and for moving functions in
“Rolling (Moving) Statistics” .
Ranking Series
EViews has an @ranks function which will generate a series based upon the ranking of another series. Ranking can be either ascending or descending depending upon whether “a” or “d” is used as an option in the function. For example to create series, ARANK, which contains the ascending ranks of the observations in the series SALES you could type:
series arank = @ranks(sales,a)
and to create a series containing the descending ranks you could type:
series drank = @ranks(sales,d)
EViews provides a number of different ways of handling ties in the ranking. For more details see
@ranks .
Missing Values
Occasionally, you will encounter data that are not available for some periods or observations, or you may attempt to perform mathematical operations where the results are undefined (e.g., division by zero, log of a negative number). EViews uses the code NA (not available) to represent these missing values.
For the most part, you need not worry about NAs. EViews will generate NAs for you when appropriate, and will automatically exclude observations with NAs from statistical calculations. For example, if you are estimating an equation, EViews will use the set of observations in the sample that have no missing values for the dependent and all of the independent variables.
There are, however, a few cases where you will need to work with NAs, so you should be aware of some of the underlying issues in the handling of NAs.
First, when you perform operations using multiple series, there may be alternative approaches for handling NAs. EViews will usually provide you with the option of casewise exclusion (common sample) or listwise exclusion (individual sample). With casewise exclusion, only those observations for which all of the series have non-missing data are used. This rule is always used, for example, in equation estimation. For listwise exclusion, EViews will use the maximum number of observations possible for each series, excluding observations separately for each series in the list of series. For example, when computing descriptive statistics for a group of series, you have the option to use a different sample for each series.
If you must work directly with NAs, just keep in mind that EViews NAs observe all of the rules of IEEE NaNs. This means that performing mathematical operations on NAs will generate missing values. Thus, each of the following expressions will generate missing values:
@log(-abs(x))
1/(x-x)
(-abs(x))^(1/3)
3*x + NA
exp(x*NA)
For the most part, comparisons involving NA values propagate NA values. For example, the commands:
series y = 3
series x = NA
series equal = (y = x)
series greater = (y > x)
will create series EQUAL and GREATER that contain NA values, since the comparison between observations in a series involving an NA yields an NA.
Note that this NA handling behavior differs from EViews 4 and earlier in which NAs were treated as ordinary values for purposes of equality (“=”) and inequality (“<>”) testing. In these versions of EViews, the comparison operators “=” and “<>” always returned a 0 or a 1. The change in behavior was deemed necessary to support the use of string missing values. In all versions of EViews, comparisons involving ordering (“>”, “<”, “<=”, “>=”) propagate NAs.
It is still possible to perform comparisons using the previous methods. One approach is to use the special functions @eqna and @neqna for performing equality and strict inequality comparisons without propagating NAs. For example, you may use the commands:
series equal1 = @eqna(x, y)
series nequal = @neqna(x, y)
so that NAs in either X or Y are treated as ordinary values for purposes of comparison. Using these two functions, EQUAL1 will be filled with the value 0, and NEQUAL will be filled with the value 1. Note that the
@eqna and
@neqna functions do not compare their arguments to NA, but rather facilitate the comparison of values so that the results are guaranteed to be 0 or 1. See also
“Version 4 Compatibility Mode” for settings that enable the previous behavior for element comparisons in programs.
To test whether individual observations in a series are NAs, you may use the @isna function. For example,
series isnaval = @isna(x)
will fill the series ISNAVAL with the value 1, since each observation in X is an NA.
There is one special case where direct comparison involving NAs does not propagate NAs. If you test equality or strict inequality against the literal NA value:
series equal2 = (x = NA)
series nequal2 = (y <> NA)
EViews will perform a special test against the NA value without propagating NA values. Note that these commands are equivalent to the comparisons involving the special functions:
series equal3 = @eqna(x, NA)
series nequal3 = @neqna(y, NA)
If used in a mathematical operation, a relational expression resulting in an NA is treated as an ordinary missing value. For example, for observations where the series X contains NAs, the mathematical expression
5*(x>3)
will yield NAs. However, if the relational expression is used as part of a sample or IF-statement, NA values are treated as FALSE.
smpl 1 1000 if x>y
smpl 1 1000 if x>y and not @isna(x) and not @isna(y)
are equivalent since the condition x>3 implicitly tests for NA values. One consequence of this behavior is that:
smpl 1 1000 if x<NA
will result in a sample with no observations since less-than tests involving NAs yield NAs.
Very early versions of EViews followed the IEEE rules for missing data with one important exception. In EViews 2 and earlier, multiplying any number by zero (including NAs) yielded a zero. In subsequent versions, the value NA times zero equals NA. Thus, an earlier recommended method of recoding (replacing) NA values in the series X no longer worked so that the command for replacing NA values with the values in Y:
x = (x<>na)*x + (x=na)*y
works in EViews 2, but does not work subsequent versions. The @nan function has been provided for this purpose.
x = @nan(x,y)
recodes NA values of X to take the values in the series Y. See
“Operators”.
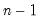 . To calculate the population standard deviation, that is division by n, use the @stdevp function. Note for symmetry purposes there is also a @stdevs which performs the same calculation as @stdev.
. To calculate the population standard deviation, that is division by n, use the @stdevp function. Note for symmetry purposes there is also a @stdevs which performs the same calculation as @stdev.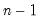 . To calculate the population standard deviation, that is division by n, use the @stdevp function. Note for symmetry purposes there is also a @stdevs which performs the same calculation as @stdev.
. To calculate the population standard deviation, that is division by n, use the @stdevp function. Note for symmetry purposes there is also a @stdevs which performs the same calculation as @stdev.