Nonlinear Two-stage Least Squares
Nonlinear two-stage least squares refers to an instrumental variables procedure for estimating nonlinear regression models involving functions of endogenous and exogenous variables and parameters. Suppose we have the usual nonlinear regression model:
 | (23.10) |
where
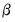
is a
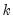
-dimensional vector of parameters, and
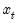
contains both exogenous and endogenous variables. In matrix form, if we have
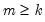
instruments
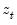
, nonlinear two-stage least squares minimizes:
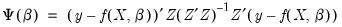 | (23.11) |
with respect to the choice of
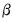
.
While there is no closed form solution for the parameter estimates, the parameter estimates satisfy the first-order conditions:
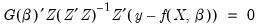 | (23.12) |
with estimated covariance given by:
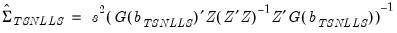 | (23.13) |
How to Estimate Nonlinear TSLS in EViews
To estimate a Nonlinear equation using TSLS simply select or Choose TSLS from the Method dropdown menu, enter your nonlinear specification and the list of instruments. Click OK.
With nonlinear two-stage least squares estimation, you have a great deal of flexibility with your choice of instruments. Intuitively, you want instruments that are correlated with the derivatives
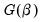
. Since
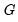
is nonlinear, you may begin to think about using more than just the exogenous and predetermined variables as instruments. Various nonlinear functions of these variables, for example, cross-products and powers, may also be valid instruments. One should be aware, however, of the possible finite sample biases resulting from using too many instruments.
Nonlinear Two-stage Least Squares with ARMA errors
While we will not go into much detail here, note that EViews can estimate non-linear TSLS models where there are ARMA error terms.
To estimate your model, simply open your equation specification window, and enter your nonlinear specification, including all ARMA terms, and provide your instrument list. For example, you could enter the regression specification:
cs = exp(c(1) + gdp^c(2)) + [ar(1)=c(3), ma(1)=c(4)]
with the instrument list:
c gov
EViews will transform the nonlinear regression model as described in
“Specifying AR Terms”, and then estimate nonlinear TSLS on the transformed specification. For nonlinear models with AR errors, EViews uses a Gauss-Newton algorithm. See
“Optimization Algorithms” for further details.
Weighted Nonlinear Two-stage Least Squares
Weights may be used in nonlinear two-stage least squares estimation, provided there are no ARMA terms. Simply add weighting to your nonlinear TSLS specification above by pressing the button and entering the weight specification (see
“Weighted Least Squares”).
The objective function for weighted TSLS is,
 | (23.14) |
The default reported standard errors are based on the covariance matrix estimate given by:
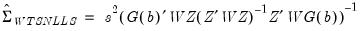 | (23.15) |
where
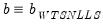
.


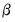 is a
is a 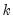 -dimensional vector of parameters, and
-dimensional vector of parameters, and 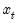 contains both exogenous and endogenous variables. In matrix form, if we have
contains both exogenous and endogenous variables. In matrix form, if we have 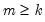 instruments
instruments 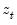 , nonlinear two-stage least squares minimizes:
, nonlinear two-stage least squares minimizes: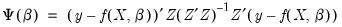
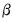 .
.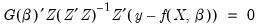
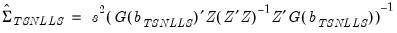
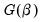 . Since
. Since 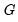 is nonlinear, you may begin to think about using more than just the exogenous and predetermined variables as instruments. Various nonlinear functions of these variables, for example, cross-products and powers, may also be valid instruments. One should be aware, however, of the possible finite sample biases resulting from using too many instruments.
is nonlinear, you may begin to think about using more than just the exogenous and predetermined variables as instruments. Various nonlinear functions of these variables, for example, cross-products and powers, may also be valid instruments. One should be aware, however, of the possible finite sample biases resulting from using too many instruments.
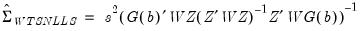
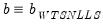 .
.