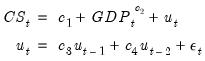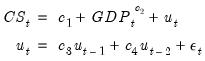Additional Topics
Dealing with Estimation Problems
Since EViews uses nonlinear estimation algorithms to estimate ARMA models, all of the discussion in
(here),
“Solving Estimation Problems”, is applicable, especially the advice to try alternative starting values.
There are a few other issues to consider that are specific to estimation of ARMA and ARFIMA models.
First, MA models are notoriously difficult to estimate. In particular, you should avoid high order MA terms unless absolutely required for your model as they are likely to cause estimation difficulties. For example, a single large autocorrelation spike at lag 57 in the correlogram does not necessarily require you to include an MA(57) term in your model unless you know there is something special happening every 57 periods. It is more likely that the spike in the correlogram is simply the product of one or more outliers in the series. By including many MA terms in your model, you lose degrees of freedom, and may sacrifice stability and reliability of your estimates.
If the underlying roots of the MA process have modulus close to one, you may encounter estimation difficulties, with EViews reporting that it cannot improve the sum-of-squares or that it failed to converge in the maximum number of iterations. This behavior may be a sign that you have over-differenced the data. You should check the correlogram of the series to determine whether you can re-estimate with one less round of differencing.
Lastly, if you continue to have problems, you may wish to turn off MA backcasting.
For a discussion of how to estimate TSLS specifications with ARMA errors, see
“Nonlinear Two-stage Least Squares”.
Nonlinear Models with ARMA errors
EViews will estimate nonlinear ordinary and two-stage least squares models with autoregressive error terms. For details, see the discussion in
“Nonlinear Least Squares”.
Weighted Models with ARMA errors
EViews does not offer built-in procedures to automatically estimate weighted models with ARMA error terms. You can, of course, always construct weighted series and then perform estimation using the weighted data and ARMA terms. Note that this procedure implies a very specific assumption about the properties of your data.
Two-Stage Regression Models with Serial Correlation
By combining two-stage least squares or two-stage nonlinear least squares with AR terms, you can estimate models where there is correlation between regressors and the innovations as well as serial correlation in the residuals.
If the original regression model is linear, EViews uses the Marquardt algorithm to estimate the parameters of the transformed specification. If the original model is nonlinear, EViews uses Gauss-Newton to estimate the AR corrected specification.
For further details on the algorithms and related issues associated with the choice of instruments, see the discussion in
“TSLS with AR errors”.
Nonlinear Models with ARMA Errors
EViews can estimate nonlinear regression models with ARMA errors. For example, suppose you wish to estimate the following nonlinear specification with an AR(2) error:
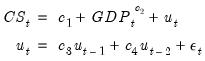 | (24.51) |
Simply specify your model using EViews expressions, followed by an additive term describing the AR correction enclosed in square brackets. The AR term should contain a coefficient assignment for each AR lag, separated by commas:
cs = c(1) + gdp^c(2) + [ar(1)=c(3), ar(2)=c(4)]
EViews transforms this nonlinear model by differencing, and estimates the transformed nonlinear specification using a Gauss-Newton iterative procedure (see
“Initializing the AR Errors”).