EViews 9.5 New Econometrics and Statistics: Estimation

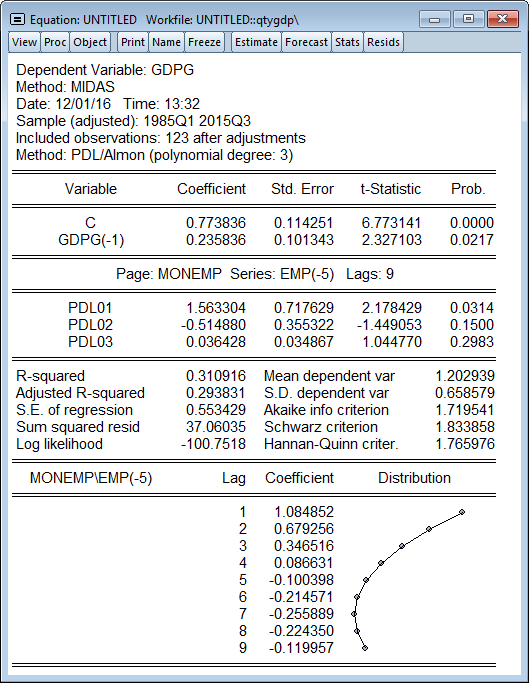
Mixed-Data Sampling (MIDAS) Regression

Mixed-Data Sampling (MIDAS) is a method of estimating and forecasting from models where the dependent variable is recorded at a lower frequency than one or more of the independent variables. Traditional approaches to dealing with the issue of mixed frequencies is to simply aggregate the higher frequency data into the lowest frequency. A significant disadvantage to this approach is that through the aggregation you discard data which can lead to less accurate estimation.

EViews workfiles natively support easy organization of mixed frequency data, and allow easy conversion from one frequency to another. EViews’ MIDAS implementation makes use of this easy handling of mixed frequencies to allow easy specification of MIDAS models.

EViews allows 4 different MIDAS weighting schemes:

• Step weights

• Almon/PDL weights

• Exponential Almon weights

• Beta weights (with or without restrictions)

EViews also offers automatic lag selection methods for determining the number of lags/periods of the higher frequency variables.

We have a complete step-by-step demonstration of MIDAS using a paper by the Federal Reserve Bank of St Louis..

Autoregressive Distributed Lag Models

EViews offers new tools for estimating and examining the properties of Autoregressive Distributed Lag (ARDL) models. ARDLs are standard least squares regressions which include lags of both the dependent variable and independent variables as regressors.

ARDL model estimation tools include:

• Built-in lag-length selection methods.

• Cointegrating relationship estimation.

• Bounds testing for long-run relationship.

ML and GLS ARMA

EViews now allows you to estimate ARMA models specified by list using ML and GLS
(in addition to the existing CLS-based estimator). Estimation of these models features
the use of the Kalman filter to evaluate the exact likelihood (Hamilton 1994).

ARFIMA

EViews supports exact maximum likelihood estimation of ARFIMA models via ML or GLS using efficient algorithms as described in Sowell (1992) and Doornik and Ooms (2003). Among the supported features are automatic intialization of the integration parameter d estimates using the Geweke and Porter-Hundlak (1983) log-periodogram regression, and concentration of the likelihood with respect to regression coefficients and scale.

Panel ARDL and Pooled Mean Group (PMG) Estimation

EViews now supports estimation of the Pooled Mean Group (PMG) estimator of Pesaran, Shin and Smith (PSS, 1999) for ARDL models with individual effects. This model is particularly popular in panel settings where the number of periods is large, since alternative GMM estimators may not be appropriate in those settings.

The PMG takes the cointegration form of the simple ARDL model and adapts it for a panel setting by allowing the intercepts, short-run coefficients and cointegrating terms to differ across cross-sections.

Threshold Regresson

EViews estimates threshold regression models (TR). This class of model includes the popular threshold autogressive models (TAR).

The Threshold Regression (TR) model describes a simple form of nonlinear regression with piecewise linear specifications and regime switching that occurs when an observed variable crosses unknown thresholds. TR specifications are quite popular as they are easy to estimate and interpret, and able to produce interesting nonlinearities and rich dynamics. Among the applications of TR are models for sample splitting, multiple equilibria, and the very popular Threshold Autoregression (TAR) and self-exciting Threshold Autoregression (SETAR) specifications (Hansen 1999, 2011; Potter 2003).

New Optimization Engine

We have integrated an all new estimation engine into many familiar EViews estimators. The new engine, which implements a sophisticated trust region approach (More and Sorensen, 1983), supports versions of the Broyden-Fletcher-Goldfarb-Shanno (BFGS), Gauss-Newton/BHHH, Newton-Raphson, and Fisher Scoring algorithms.

In addition to providing alternative tools for optimization, the new engine allows for the computation of numeric second derivatives and provides support for a number of alternative ordinary and robust coefficient covariance matrix estimators.

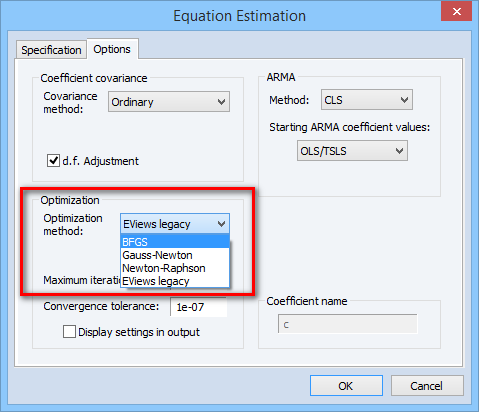
The following EViews estimators have been updated to support the new estimation engine model estimation tools include:

• Single equation nonlinear least squares and ARMA

• Binary

• Count

• Ordered

• Censored

• ARCH (equation and system)

• Switching Regression

• GLM

• Heckman Selection

• FIML

• State Space

• Logl

FIML with Variance Restrictions

The system FIML estimator now has an option specifying the form of the residual covariance matrix used in estimation. You may choose between:

• unrestricted

• diagonal

• user-specified

If you choose the user-specified, you must also provide the name of a Sym object containing values for all of the residual variances and covariances.

Following estimation, EViews offers you the ability to examine the covariance matrix used in estimation.